
分析 (1)先通过特殊值,比较两数的大小,再猜想,构造函数,利用函数的单调性和最值比较大小;
(2)利用用导数,讨论导函数在(a,1)上正负性,判断f(x)在(a,1)上的单调性.
解答 解;(Ⅰ)当a=0时,f(x)=x2lnx,
f(1)=0,f(e)=e2>e(e-1),猜想f(x)≥x(x-1),下面证明
f(x)-x(x-1)=x2lnx-x(x-1)≥0,?$lnx≥\frac{x-1}{x}$,定义域为(0,+∞)
令g(x)=$lnx-\frac{x-1}{x}$,g′(x)=$\frac{1}{x}-\frac{1}{{x}^{2}}$=$\frac{x-1}{{x}^{2}}$
∴g(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
∴g(x)≥g(1)=0,即f(x)≥x(x-1);
(Ⅱ)f′(x)=$(x-a)(2lnx+1-\frac{a}{x})$,令h(x)=$2lnx+1-\frac{a}{x}$
∴${h}^{′}(x)=\frac{2}{x}+\frac{a}{{x}^{2}}$>0,即h(x)在(0,+∞)上单调递增,
又h(a)=2lna<0,h(1)=1-a>0,存在唯一x0∈(a,1),使h(x0)=0,
当0<x<x0时,h(x)<0,当x>x0时,h(x)>0
于是0<x<a时,f′(x)>0;a<x<x0时,f′(x)<0,x>x0时,f′(x)>0
即f(x)在(0,a)上单调递增,在(a,x0)上递减,在(x0,+∞)上单调递增,从而在(x0,1)上单调递增,
故f(x)在(a,1)上唯一极小值点.
点评 本题考查了导数在证明不等式中的运用,运用了等价转化,分类讨论思想,是一道导数的综合应用题.属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
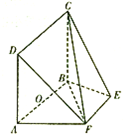 如图,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD所在平面与平面ABEF互相垂直.
如图,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD所在平面与平面ABEF互相垂直.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com