
分析 (1)运用等差数列的通项和求和公式及等比数列的通项,列方程,解得即可得到所求通项;
(2)化简所求数列,结合裂项相消求和和等比数列的求和公式,化简整理即可得到.
解答 解:(1)设等差数列{an}的公差为d,
则$\left\{\begin{array}{l}{{a}_{1}+2q=3}\\{{a}_{1}+d+2q=6}\\{5{a}_{1}+\frac{5×4}{2}d=40}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=2}\\{d=3}\\{q=\frac{1}{2}}\end{array}\right.$,
所以an=2+3(n-1)=3n-1,
bn=$\frac{1}{2}$•($\frac{1}{2}$)n-1=($\frac{1}{2}$)n;
(2)$\frac{1}{{a}_{n}{a}_{n+1}}$+$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{3}$($\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n+1}}$)+$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{3}$($\frac{1}{3n-1}$-$\frac{1}{3n+2}$)+22n+1,
即有Tn=$\frac{1}{3}$[($\frac{1}{2}-\frac{1}{5}$)+($\frac{1}{5}-\frac{1}{8}$)+…+($\frac{1}{3n-1}$-$\frac{1}{3n+2}$)]+$\frac{8(1-{4}^{n})}{1-4}$
=$\frac{1}{3}$($\frac{1}{2}$-$\frac{1}{3n+2}$)+$\frac{1}{3}$(22n+3-8)
=$\frac{1}{3}$(22n+3-$\frac{1}{3n+2}$)-$\frac{5}{2}$.
点评 本题考查等差数列和等比数列的通项和求和公式的运用,同时考查裂项相消求和,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
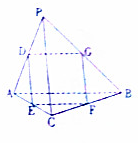 如图,已知三棱锥P-ABC中,点D,E,F,G分别是棱AP,AC,BC,PB上的点,若PA=PB=PC=$\sqrt{2}$,AB=AC=BC=1,且$\frac{AE}{AC}$=$\frac{AD}{AP}$=$\frac{BF}{BC}$=$\frac{BG}{BP}$.
如图,已知三棱锥P-ABC中,点D,E,F,G分别是棱AP,AC,BC,PB上的点,若PA=PB=PC=$\sqrt{2}$,AB=AC=BC=1,且$\frac{AE}{AC}$=$\frac{AD}{AP}$=$\frac{BF}{BC}$=$\frac{BG}{BP}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
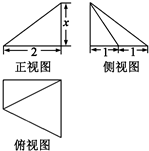
| A. | 2 | B. | 3 | C. | $\frac{4}{15}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com