
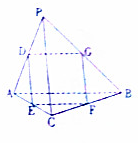
 如图,已知三棱锥P-ABC中,点D,E,F,G分别是棱AP,AC,BC,PB上的点,若PA=PB=PC=$\sqrt{2}$,AB=AC=BC=1,且$\frac{AE}{AC}$=$\frac{AD}{AP}$=$\frac{BF}{BC}$=$\frac{BG}{BP}$.
如图,已知三棱锥P-ABC中,点D,E,F,G分别是棱AP,AC,BC,PB上的点,若PA=PB=PC=$\sqrt{2}$,AB=AC=BC=1,且$\frac{AE}{AC}$=$\frac{AD}{AP}$=$\frac{BF}{BC}$=$\frac{BG}{BP}$.分析 (1)由$\frac{AE}{AC}$=$\frac{AD}{AP}$=$\frac{BF}{BC}$=$\frac{BG}{BP}$,得出DE∥GF,DG∥EF,判断四边形DEFG是平行四边形;
再利用等腰三角形底边的中线,判断平行四边形DEFG是矩形,从而求出矩形DEFG面积的最大值;
(2)利用该三棱锥的对称性,得出在(1)的条件下存在点Q,到三棱锥P-ABC六条棱的中点的距离相等.
解答 解:(1)三棱锥P-ABC中,$\frac{AE}{AC}$=$\frac{AD}{AP}$,∴DE∥PC,
$\frac{BF}{BC}$=$\frac{BG}{BP}$,∴GF∥PC,
∴DE∥GF;
同理,DG∥EF,
∴四边形DEFG是平行四边形;
又取AB的中点M,连接PM、CM,∴PM⊥AB,CM⊥AB,
如图1所示;
且PM∩CM=M,
∴AB⊥平面PCM,
又PC?平面PCM,
∴AB⊥PC,
又AB∥EF,DE∥PC,
∴EF⊥DE,
平行四边形DEFG是矩形;
在矩形DEFG中,
∵$\frac{DE}{PC}$=$\frac{AE}{AC}$,∴DE=$\frac{PC}{AC}$•AE=$\sqrt{2}$AE;
又∵$\frac{EF}{AB}$=$\frac{CE}{AC}$,∴EF=$\frac{AB}{AC}$•CE=CE;
∴矩形DEFG的面积为S矩形DEFG=DE•EF=$\sqrt{2}$AE•CE
当AE=CE=$\frac{1}{2}$AC=$\frac{1}{2}$时,S矩形DEFG的面积最大,
最大值为$\sqrt{2}$×$\frac{1}{2}$×$\frac{1}{2}$=$\frac{\sqrt{2}}{4}$;
(2)在(1)的条件下存在点Q,到三棱锥P-ABC六条棱的中点的距离相等;
理由是:连接DF、EG,设Q为EG的中点,
则DF∩EG=Q,且QD=QE=QF=QG=$\frac{1}{2}$EG;
分别取AB、PC的中点M、N,连接ME、NE、MG、NG、MN,如图2所示;
与(1)同理可证,四边形MENG是矩形,其对角线的交点是EG的中点Q,
且QM=QN=$\frac{1}{2}$EG;
所以,Q为满足条件的点.
点评 本题考查了空间中的平行与垂直关系的应用问题,也考查了空间想象能力与逻辑思维能力,是综合性题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com