某种产品的加工需要5道工序.问如果其中某一工序不能放在最后.有多少种排列加工顺序的方法? 题目和参考答案——青夏教育精英家教网—

6．某种产品的加工需要5道工序，问如果其中某一工序不能放在最后，有多少种排列加工顺序的方法？

分析根据题意，假设有5个位置对应5道工序，设不能放在最后的工序为A；分2步进行分析，先分析A的安排方法数目，再在剩余的4个位置安排其余4道工序，分别求出每一步的安排方法数目，进而由分步计数原理计算可得答案．

解答解：根据题意，假设有5个位置对应5道工序，
设不能放在最后的工序为A，则A有4个位置可选，
在剩余的4个位置安排其余4道工序，有A₄⁴=24种情况，
则共有4×24=96种排列加工顺序的方法；
答：某一工序不能放在最后，有96种排列加工顺序的方法．

点评本题考查排列的运用，解题时注意解题的规范性，最好设出受到限制的工序为A．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

16．

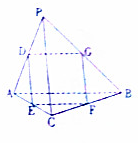如图，已知三棱锥P-ABC中，点D，E，F，G分别是棱AP，AC，BC，PB上的点，若PA=PB=PC=$\sqrt{2}$，AB=AC=BC=1，且$\frac{AE}{AC}$=$\frac{AD}{AP}$=$\frac{BF}{BC}$=$\frac{BG}{BP}$．
（1）判断四边形DEFG的形状并求其面积的最大值；
（2）在（1）的条件下是否存在点Q，到三棱锥P-ABC六条棱的中点相等．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

17．函数y=2cos（$\frac{π}{3}$-$\frac{1}{2}$x），则该函数的最小正周期为4π，对称轴方程为x=$\frac{2π}{3}$+2kπ，k∈Z，单调递增区间是[4kπ-$\frac{4π}{3}$，4kπ+$\frac{2π}{3}$]，k∈Z，．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

14．设方程组$\left\{\begin{array}{l}{{x}^{3}-xyz=-5}\\{{y}^{3}-xyz=2}\\{{z}^{3}-xyz=21}\end{array}\right.$的正实数解为（x，y，z），则x+y+z=6．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

1．

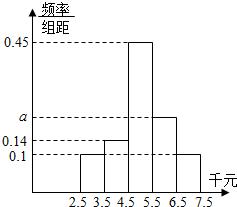两会结束后，房价问题仍是国民关注的热点问题，某高校金融学一班的学生对某城市居民对房价的承受能力（如能买每平方米6千元的房子即承受能力为6千元）的调查作为社会实践，进行调查统计，将承受能力数据按区间[2.5，3.5），[3.5，4.5），[4.5，5.5），[5.5，6.5），[6.5，7.5]（千元）进行分组，得到如下统计图：
（1）求a的值，并估计该城市居民的平均承受能力是多少元；
（2）若用分层抽样的方法，从承受能力在[3.5，4.5）与[5.5，6.5）的居民中抽取5人，在抽取的5人中随机取2人，求2人的承受能力不同的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

11．一个算法的程序框图如图所示，若该程序输出的结果为$\frac{5}{6}$，则判断框中应填入的条件是（　　）