
分析 (Ⅰ)先求导,再根据函数的单调性即可求出最小值;
(Ⅱ)求出g′(x),得到h(x)再求导,根据条件②得到方程组,继而得${{x}_{0}}^{2}+2{x}_{0}+20b-4=0$(*),根据判别式求出b的值,继而得到函数h(x)的解析式,
再根据条件①,进行分类讨论,利用函数最值求出a的值,函数g(x)的解析式即可求出.
解答 解:(Ⅰ)∵y=f(2x)-2x,
∴y′=2e2x-1-2,
由y′≤0,得到x≤$\frac{1}{2}$,∴函数y在(-∞,$\frac{1}{2}$)上为减函数,
由y′>0,得到x>$\frac{1}{2}$,∴函数y在($\frac{1}{2}$,+∞)上为增函数,
∴x=$\frac{1}{2}$时,ymin=0;
(Ⅱ)∵g′(x)=3x2-a,
∴h(x)=3ex+2n-3n(x2+4x+20b),
∴h′(x)=3ex+2n-3n(2x+4),
由条件②得$\left\{\begin{array}{l}{{e}^{{x}_{0}+2n}=n(2{x}_{0}+4),(i)}\\{{e}^{{x}_{0}+2n}=n({{x}_{0}}^{2}+4{x}_{0}+20b),(ii)}\end{array}\right.$
∴n(${{x}_{0}}^{2}+4{x}_{0}+20b$)=n(2x0+4),
由(i)知n≠0,
∴${{x}_{0}}^{2}+4{x}_{0}+20b$=2x0+4,
即${{x}_{0}}^{2}+2{x}_{0}+20b-4=0$(*),
由条件(2)知,方程(*)的判别式△=4-4(20b-4)=0,
∴b=$\frac{1}{4}$,x0=-1,
代入(i)有e2n-1-2n=0,由第(I)小题知,函数y=e2x-1-2x有最小值0,当且仅当x=$\frac{1}{2}$取到最小值0,
∴方程e2n-1-2n=0有唯一解n=$\frac{1}{2}$,
∴h(x)=3ex+1-$\frac{3}{2}$(x2+4x+5),
由b=$\frac{1}{4}$得g(x)=x3-ax+$\frac{1}{4}$,
∴g′(x)=3x2-a,当a≤0时,g′(x)>0,
∴g(x)在[-1,1]上为增函数,
由条件①知,只需g(-1)≥0即a≥$\frac{3}{4}$,这与a≤0矛盾;
当a>0时,由g′(x)>0,得到x<-$\sqrt{\frac{a}{3}}$,或x>$\sqrt{\frac{a}{3}}$,
由g′(x)≤0,得到-$\sqrt{\frac{a}{3}}$≤x≤$\sqrt{\frac{a}{3}}$,
因此若a≥3,x∈[-1,1]时g′(x)≤0,
∴g(x)在[-1,1]上为减函数由条件①知只需g(1)≥0即a≤$\frac{5}{4}$,这与a≥3矛盾;
若0<a<3时,
∵-$\sqrt{\frac{a}{3}}$>-1,$\sqrt{\frac{a}{3}}$<1,
∴-$\sqrt{\frac{a}{3}}$,$\sqrt{\frac{a}{3}}$分别是(-1,1)内的极大值点,极小值点
由条件①知只需$\left\{\begin{array}{l}{g(\sqrt{\frac{a}{3}})≥0}\\{g(-1)≥0}\end{array}\right.$,
解得a=$\frac{3}{4}$,与0<a<3相符,
∴g(x)=x3-$\frac{3}{4}$x+$\frac{1}{4}$,
综上可得:g(x)=x3-$\frac{3}{4}$x+$\frac{1}{4}$,h(x)=3ex+1-$\frac{3}{2}$(x2+4x+5).
点评 本题考查了导数和函数的单调性极值最值的关系,考查了分类讨论的思想,划归思想,方程思想,培养了学生得运算能力,推理论证能力,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体ABC-A1B1C1中,侧面AA1B1B⊥底面A1B1C1,四边形AA1B1B是矩形,A1C1=A1B1,∠B1A1C1=120°,BC∥B1C1,B1C1=2BC.
如图,在多面体ABC-A1B1C1中,侧面AA1B1B⊥底面A1B1C1,四边形AA1B1B是矩形,A1C1=A1B1,∠B1A1C1=120°,BC∥B1C1,B1C1=2BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
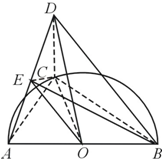 如图,已知点C是圆心为O半径为1的半圆弧上从点A数起的第一个三等分点,AB是直径,CD=1,CD⊥平面ABC,点E是AD的中点.
如图,已知点C是圆心为O半径为1的半圆弧上从点A数起的第一个三等分点,AB是直径,CD=1,CD⊥平面ABC,点E是AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com