
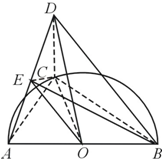
 如图,已知点C是圆心为O半径为1的半圆弧上从点A数起的第一个三等分点,AB是直径,CD=1,CD⊥平面ABC,点E是AD的中点.
如图,已知点C是圆心为O半径为1的半圆弧上从点A数起的第一个三等分点,AB是直径,CD=1,CD⊥平面ABC,点E是AD的中点.分析 (1)建立空间坐标系,求出平面的法向量,利用向量法即可求二面角O-EC-B的余弦值.
(2)方法一:利用向量法即可求点C到平面ABD的距离.
方法二:根据点到平面的定义求出点到平面的垂线段,即可.
解答 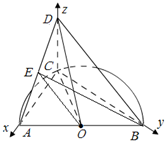 解:(1)∵C是圆心为O半径为1的半圆弧上
解:(1)∵C是圆心为O半径为1的半圆弧上
从点A数起的第一个三等分点,∴∠AOC=60°,
∴△OAC是等边三角形,∴CA=CD=1.
∵C是圆周上的点,AB是直径,
∴AC⊥AB,∴$CB=\sqrt{A{B^2}-C{A^2}}=\sqrt{3}$,
又CD⊥平面ABC,
∴AC,BC,CD两两垂直.以点C为坐标原点,$\overrightarrow{CA}$、$\overrightarrow{CB}$、$\overrightarrow{CD}$分别为x、y、z轴的正向,建立空间直角坐标系,
则A(1,0,0),$B(0,\sqrt{3},0)$,C(0,0,0),D(0,0,1),$E({\frac{1}{2},0,\frac{1}{2}})$,$O(\frac{1}{2},\frac{{\sqrt{3}}}{2},0)$,
于是,$\overrightarrow{CB}=(0,\sqrt{3},0)$,$\overrightarrow{CE}=(\frac{1}{2},0,\frac{1}{2})$,$\overrightarrow{CO}=(\frac{1}{2},\frac{{\sqrt{3}}}{2},0)$.
设n=(x,y,z)为平面BCE的法向量,m=(p,q,r)为平面OCE的法向量,$n•\overrightarrow{CB}=0⇒y=0$,$n•\overrightarrow{CE}=0⇒\frac{1}{2}x+\frac{1}{2}z=0$,取x=1得n=(1,0,-1).$m•\overrightarrow{CE}=0⇒\frac{1}{2}p+\frac{1}{2}r=0$,$m•\overrightarrow{CO}=0⇒\frac{1}{2}p+\frac{{\sqrt{3}}}{2}q=0$,
取p=1得$m=(1,-\frac{{\sqrt{3}}}{3},-1)$
$cosθ=\frac{n•m}{|n||m|}=\frac{{1×1+0×(-\frac{{\sqrt{3}}}{3})+(-1)×(-1)}}{{\sqrt{{1^2}+{0^2}+{{(-1)}^2}}•\sqrt{{1^2}+{{(-\frac{{\sqrt{3}}}{3})}^2}+{{(-1)}^2}}}}=\frac{{\sqrt{42}}}{7}$,
因此,二面角O-EC-B的余弦值是$\frac{{\sqrt{42}}}{7}$.
(2)方法一:由(1)知$\overrightarrow{AB}=(-1,\sqrt{3},0),\overrightarrow{AD}=(-1,0,1),\overrightarrow{CD}=(0,0,1)$,
设h=(x1,y1,z1)为平面ABD的法向量,则$\left\{\begin{array}{l}\overrightarrow{AB}•h=0\\ \overrightarrow{AD}•h=0\end{array}\right.$,即$\left\{\begin{array}{l}-{x_1}+\sqrt{3}{y_1}=0\\-{x_1}+{z_1}=0\end{array}\right.$,取${y_1}=\sqrt{3}$得$h=(3,\sqrt{3},3)$.
设向量h和$\overrightarrow{CD}$所成的角为?,则$cos?=\frac{{h•\overrightarrow{CD}}}{{|h||{\overrightarrow{CD}}|}}=\frac{{3×0+\sqrt{3}×0+3×1}}{{\sqrt{{3^2}+{{\sqrt{3}}^2}+{3^2}}×1}}=\frac{{\sqrt{21}}}{7}$,
设点C到平面ABD的距离为d,则$d=|\overrightarrow{CD}|cos?=\frac{{\sqrt{21}}}{7}$.
方法二:由(1)知AC=1,$BC=\sqrt{3}$
因为直线CD⊥平面ABC,所以,CD⊥AC,CD⊥BC,
于是,$AD=\sqrt{A{C^2}+C{D^2}}=\sqrt{{1^2}+{1^2}}=\sqrt{2}$,$BD=\sqrt{B{C^2}+C{D^2}}=\sqrt{3+1}=2$.
因为AB=2=BD,点E是AD的中点,所以BE⊥AD.
因此,$BE=\sqrt{A{B^2}-A{E^2}}=\sqrt{{2^2}-{{({\frac{{\sqrt{2}}}{2}})}^2}}=\sqrt{\frac{7}{2}}$,
从而,${S_{△ABC}}=\frac{1}{2}AC•BC=\frac{1}{2}×1×\sqrt{3}=\frac{{\sqrt{3}}}{2}$,
${S_{△ABD}}=\frac{1}{2}AD•BE=\frac{1}{2}×\sqrt{2}×\sqrt{\frac{7}{2}}=\frac{{\sqrt{7}}}{2}$.
因为,VC-ABD=VD-ABC,
设点C到平面ABD的距离为h,
则有$\frac{1}{3}{S_{△ABD}}•h=\frac{1}{3}{S_{△ABC}}•CD$,
即$\frac{{\sqrt{7}}}{2}•h=\frac{{\sqrt{3}}}{2}×1$,
于是,$h=\frac{{\sqrt{21}}}{7}$.
点评 本题主要考查二面角的求解以及点到平面的距离的计算,建立坐标系,利用向量法是解决空间二面角和点到平面距离的常用方法.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.
如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 获取消息渠道 | 看电视 | 收听广播 | 其它渠道 |
| 男性 | 480 | m | 180 |
| 女性 | 384 | 210 | 90 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com