
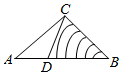
 如图,B、C两点之间不能直接到达,为测量B、C两点间的距离(单位:千米),先确定一条直线AD,使得A、D、B三点共线,且∠ADC为钝角,现测得∠BCD=60°,∠A=45°,CD=$\sqrt{6}$-$\sqrt{2}$,AC=$\sqrt{2}$,∠CDB=θ.
如图,B、C两点之间不能直接到达,为测量B、C两点间的距离(单位:千米),先确定一条直线AD,使得A、D、B三点共线,且∠ADC为钝角,现测得∠BCD=60°,∠A=45°,CD=$\sqrt{6}$-$\sqrt{2}$,AC=$\sqrt{2}$,∠CDB=θ.分析 (Ⅰ)由正弦定理可得∠ACD的大小以及B、C两点间的距离;
(Ⅱ)求函数f(x)=|AD|sin(2x+∠B)(x∈[0,θ])的表达式,即可求出函数的最值.
解答 解:(Ⅰ)由正弦定理可得$\frac{AC}{sin∠ADC}=\frac{CD}{sinA}$,
∴sin∠ADC=$\frac{\sqrt{2}×\frac{\sqrt{2}}{2}}{\sqrt{6}-\sqrt{2}}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$,
∵∠ADC为钝角,
∴∠ADC=105°,
∴∠ACD=30°.
∵∠ACB=90°,∠B=45°,
∴BC=AC=$\sqrt{2}$.
(Ⅱ)由正弦定理可得$\frac{\sqrt{6}-\sqrt{2}}{\frac{\sqrt{2}}{2}}=\frac{AD}{\frac{1}{2}}$,∴AD=$\sqrt{3}$-1.
∴f(x)=|AD|sin(2x+∠B)=($\sqrt{3}$-1)sin(2x+45°),
∵x∈[0°,75°],
∴2x+45°∈[45°,195°],
∴x=75°时,f(x)取得最小值=($\sqrt{3}$-1)×$\frac{\sqrt{2}-\sqrt{6}}{4}$=$\frac{\sqrt{3}-2\sqrt{2}}{2}$;
x=22.5°时,f(x)取得最大值=$\sqrt{3}$-1.
点评 本题考查正弦定理的运用,考查三角函数知识,考查学生的计算能力,正确求出∠ADC是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{12}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com