
分析 (1)根据完全平方和公式展开(a+b+c)2,然后将a+b+c=0,a2+b2+c2=1整体代入来求ab+bc+ca的值;
(2)根据完全平方和公式展开(a+b+c)4,然后将a+b+c=0,ab+bc+ca=-$\frac{1}{2}$整体代入来求a4+b4+c4的值.
解答 解:(1)∵a+b+c=0,
∴(a+b+c)2=0,即a2+b2+c2+2ab+2bc+2ca=0,
∴a2+b2+c2+2(ab+bc+ca)=0,①
∵a2+b2+c2=1,②
把②代入①,得:
1+2(ab+bc+ca)=0,
解得,ab+bc+ca=-$\frac{1}{2}$;
(2)∵a4+b4+c4
=(a2+b2+c2)2-2(a2b2+b2c2+c2a2)
=(a2+b2+c2)2-2[(ab+bc+ac)2-2abc(a+b+c)],
ab+bc+ca=-$\frac{1}{2}$,a+b+c=0,
∴a4+b4+c4
=1-2×[(-$\frac{1}{2}$)2-0]
=$\frac{1}{2}$.
点评 本题主要考查完全平方公式的变形,熟记公式结构是解题的关键.完全平方公式:(a±b)2=a2±2ab+b2.另外,本题还利用了“整体代入”法.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日销售量(台) | 100 | 150 | 200 |
| 频数 | 10 | 25 | 15 |
| 频率 | 0.2 | 0.5 | 0.3 |
| 日销售量(台) | 100 | 150 | 200 |
| 频数 | 15 | 15 | 20 |
| 频率 | 0.3 | 0.3 | 0.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
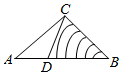 如图,B、C两点之间不能直接到达,为测量B、C两点间的距离(单位:千米),先确定一条直线AD,使得A、D、B三点共线,且∠ADC为钝角,现测得∠BCD=60°,∠A=45°,CD=$\sqrt{6}$-$\sqrt{2}$,AC=$\sqrt{2}$,∠CDB=θ.
如图,B、C两点之间不能直接到达,为测量B、C两点间的距离(单位:千米),先确定一条直线AD,使得A、D、B三点共线,且∠ADC为钝角,现测得∠BCD=60°,∠A=45°,CD=$\sqrt{6}$-$\sqrt{2}$,AC=$\sqrt{2}$,∠CDB=θ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 3 | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com