
| A. | $m=\frac{π}{6},M=\frac{π}{3}$ | B. | $m=\frac{π}{3},M=\frac{2π}{3}$ | C. | $m=\frac{4π}{3},M=2π$ | D. | $m=\frac{2π}{3},M=\frac{4π}{3}$ |
分析 利用两角差的正弦化简得,f(x)=sin($x-\frac{π}{3}$),由函数f(x)在$[a-\frac{π}{3},b-\frac{π}{3}]$上的值域为$[-\frac{1}{2},1]$,不妨设$a-\frac{π}{3}=-\frac{π}{6}$,可得b-$\frac{π}{3}$∈[$\frac{π}{2},\frac{7}{6}π$],由此可得b-a的最大值M和最小值m的值.
解答 解:$f(x)=\frac{1}{2}sinx-\frac{{\sqrt{3}}}{2}cosx$=sin($x-\frac{π}{3}$),
∵x∈[a,b](b>a),∴$x-\frac{π}{3}∈[a-\frac{π}{3},b-\frac{π}{3}]$,
由函数f(x)在$[a-\frac{π}{3},b-\frac{π}{3}]$上的值域为$[-\frac{1}{2},1]$,
不妨设$a-\frac{π}{3}=-\frac{π}{6}$,则b-$\frac{π}{3}$∈[$\frac{π}{2},\frac{7}{6}π$],
∴b-a的最大值M=$\frac{7}{6}π-(-\frac{π}{6})=\frac{4π}{3}$;
最小值m=$\frac{π}{2}-(-\frac{π}{6})=\frac{2π}{3}$.
故选:D.
点评 本题考查两角差的正弦,考查了三角函数的值是基础题.


科目:高中数学 来源: 题型:选择题
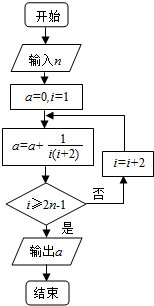
| A. | $\frac{2015}{4031}$ | B. | $\frac{4030}{4031}$ | C. | $\frac{2014}{4029}$ | D. | $\frac{2015}{4029}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
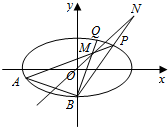 如图,已知椭圆C:$\frac{x^2}{2}$+y2=1,点B坐标为(0,-1),过点B的直线交椭圆C于y轴左侧另外一点A,且线段AB的中点E在直线y=x上.
如图,已知椭圆C:$\frac{x^2}{2}$+y2=1,点B坐标为(0,-1),过点B的直线交椭圆C于y轴左侧另外一点A,且线段AB的中点E在直线y=x上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{13}{6}$ | C. | $\frac{7}{3}$ | D. | $\frac{15}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
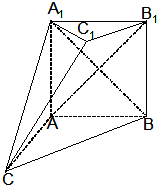 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,△A1CB是等边三角形,AC=AB=1,B1C1∥BC,BC=2B1C1
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,△A1CB是等边三角形,AC=AB=1,B1C1∥BC,BC=2B1C1查看答案和解析>>
科目:高中数学 来源: 题型:选择题
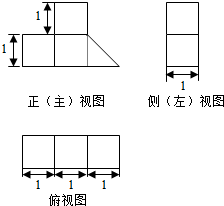
| A. | $\frac{7}{3}$ m3 | B. | $\frac{9}{2}$ m3 | C. | $\frac{9}{4}$ m3 | D. | $\frac{7}{2}$ m3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com