考点:命题的真假判断与应用
专题:综合题,简易逻辑
分析:(1)函数y=
和
y=x是同一个函数,可从定义域与对应法则两个方面判断;
(2)f(x)=
(x∈[2,6])的值域为
(,2),根据函数的单调性求出值域与题设中相对照;
(3)既奇又偶的函数只有f(x)=0,由于定义域不同时,对应法则相同两函数也不是同一函数,故可举例定义域相同对应法则不同的函数例证;
(4)集合{x∈
=
,a∈N
*}中只有四个元素的判断,可列举出集合中的元素进行判断;
解答:
解:1)函数y=
和
y=x的定义域都是(-∞,0),但y=
=
y=-x与函数
y=x的解析式不一样,即对应法则不同,故不是同一个函数,故不是真命题;
(2)f(x)=
(x∈[2,6])是一个减函数,其值域为
[,2],不是
(,2),故不是真命题;
(3)既奇又偶的函数只有f(x)=0不对,因为f(x)=0(∈[-2,2])是一个即奇又偶的函数,故不是真命题;
(4)集合{x∈N|x=
,a∈N
*}中只有四个元素1,2,3,6,故是真命题;
综上,正确的命题仅有④,
故答案为④.
点评:本题考查命题真假的判断,此类题涉及到的知识点较多,知识跨度大,需要有着比较扎实的知识与技能功底才能正确判断.



 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案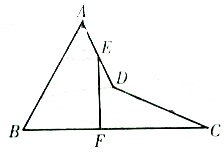 如图,在空间四边形ABCD中,两条对边AB=CD=3,E、F分别是另外两条对边AD,BC上的点,
如图,在空间四边形ABCD中,两条对边AB=CD=3,E、F分别是另外两条对边AD,BC上的点,