
【题目】已知定义在![]() 上的函数
上的函数![]() 和数列
和数列![]() 满足下列条件:
满足下列条件:![]() ,
,![]() ,当
,当![]() 且
且![]() 时,
时,![]() 且
且![]() ,其中
,其中![]() 、
、![]() 均为非零常数.
均为非零常数.
(1)若![]() 是等差数列,求实数
是等差数列,求实数![]() 的值;
的值;
(2)令![]() (
(![]() ),若
),若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)令![]() (
(![]() ),若
),若![]() ,数列
,数列![]() 满足
满足![]() ,若数列
,若数列![]() 有最大值
有最大值![]() ,最小值
,最小值![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分)某公司生产的商品A每件售价为5元时,年销售10万件,
(1)据市场调查,若价格每提高一元,销量相应减少1万件,要使销售收入不低于原销售收入,该商品的销售价格最多提高多少元?
(2)为了扩大该商品的影响力,公司决定对该商品的生产进行技术革新,将技术革新后生产的商品售价提高到每件![]() 元,公司拟投入
元,公司拟投入![]() 万元作为技改费用,投入
万元作为技改费用,投入![]() 万元作为宣传费用。试问:技术革新后生产的该商品销售量m至少应达到多少万件时,才可能使技术革新后的该商品销售收入等于原销售收入与总投入之和?
万元作为宣传费用。试问:技术革新后生产的该商品销售量m至少应达到多少万件时,才可能使技术革新后的该商品销售收入等于原销售收入与总投入之和?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机和电子阅读器越来越普及,人们的阅读习惯也发生了改变,手机和电子阅读产品方便易携带,越来越多的人习惯通过手机或电子阅读器阅读.某电子书阅读器厂商随机调查了![]() 人,统计了这
人,统计了这![]() 人每日平均通过手机或电子阅读器阅读的时间(单位:分钟),由统计数据得到如下频率分布直方图,已知阅读时间在
人每日平均通过手机或电子阅读器阅读的时间(单位:分钟),由统计数据得到如下频率分布直方图,已知阅读时间在![]() ,
, ![]() ,
, ![]() 三组对应的人数依次成等差数列.
三组对应的人数依次成等差数列.
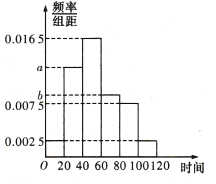
(1)求频率分布直方图中![]() ,
, ![]() 的值;
的值;
(2)若将日平均阅读时间不少于![]() 分钟的用户定义为“电子阅读发烧友”,将日平均阅读时间少于
分钟的用户定义为“电子阅读发烧友”,将日平均阅读时间少于![]() 分钟的用户定义为“电子阅读潜在爱好者”,现从上述“电子阅读发烧友”与“电子阅读潜在爱好者”的人中按分层抽样选出
分钟的用户定义为“电子阅读潜在爱好者”,现从上述“电子阅读发烧友”与“电子阅读潜在爱好者”的人中按分层抽样选出![]() 人,再从这
人,再从这![]() 人中任取
人中任取![]() 人,求恰有
人,求恰有![]() 人为“电子阅读发烧友”的概率.
人为“电子阅读发烧友”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,离心率等于![]() ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线![]() 的焦点.
的焦点.
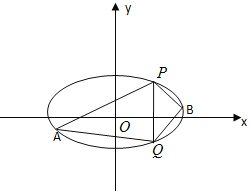
(Ⅰ)求椭圆C的方程;
(Ⅱ)点P(2,3), Q(2,-3)在椭圆上,A,B是椭圆上位于直线PQ两恻的动点,
①若直线AB的斜率为![]() ,求四边形APBQ面积的最大值;
,求四边形APBQ面积的最大值;
②当A、B运动时,满足于∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中, ![]() 是坐标原点,设函数
是坐标原点,设函数![]() 的图象为直线
的图象为直线![]() ,且
,且![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,给出下列四个命题:
两点,给出下列四个命题:
①存在正实数![]() ,使
,使![]() 的面积为
的面积为![]() 的直线
的直线![]() 仅有一条;
仅有一条;
②存在正实数![]() ,使
,使![]() 的面积为
的面积为![]() 的直线
的直线![]() 仅有二条;
仅有二条;
③存在正实数![]() ,使
,使![]() 的面积为
的面积为![]() 的直线
的直线![]() 仅有三条;
仅有三条;
④存在正实数![]() ,使
,使![]() 的面积为
的面积为![]() 的直线
的直线![]() 仅有四条.
仅有四条.
其中,所有真命题的序号是( ).
A. ①②③ B. ③④ C. ②④ D. ②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象过原点,且在
的图象过原点,且在![]() 处取得极值,直线
处取得极值,直线![]() 与曲线
与曲线![]() 在原点处的切线互相垂直.
在原点处的切线互相垂直.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)若对任意实数的![]() ,恒有
,恒有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com