

分析 (1)由题意即可确定θ的取值范围.
(2)连接BD,过D作地面的垂线,垂足为E,在Rt△BDE中,可求∠DBE=θ+$\frac{π}{6}$,DB=2,解三角形即可解得f(θ).
解答 解:(1)BC与地面所成的角,就是直线与平面所成的角,显然角θ的范围是[0,$\frac{π}{2}$].
(2)连接BD,则∠DBC=$\frac{π}{6}$,过D作地面的垂线,垂足为E,在Rt△BDE中,∠DBE=θ+$\frac{π}{6}$,DB=2,
∴f(θ)=2sin(θ+$\frac{π}{6}$),(0$≤θ≤\frac{π}{2}$).
点评 本题主要考查了解三角形,考查了在实际问题中建立三角函数模型,正确做出辅助线是解题的关键,属于基本知识的考查.


科目:高中数学 来源:2017届四川成都七中高三10月段测数学(文)试卷(解析版) 题型:填空题
已知三次函数 ,下列命题正确的是 .
,下列命题正确的是 .
①函数 关于原点
关于原点 中心对称;
中心对称;
②以 ,
, 两不同的点为切点作两条互相平行的切线,分别与
两不同的点为切点作两条互相平行的切线,分别与 交于
交于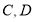 两点,则这四个点的横坐标满足关系
两点,则这四个点的横坐标满足关系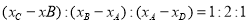 ;
;
③以 为切点,作切线与
为切点,作切线与 图像交于点
图像交于点 ,再以点
,再以点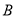 为切点作直线与
为切点作直线与 图像交于点
图像交于点 ,再以点
,再以点 作切点作直线与
作切点作直线与 图像交于点
图像交于点 ,则
,则 点横坐标为
点横坐标为 ;
;
④若 ,函数
,函数 图像上存在四点
图像上存在四点 ,使得以它们为顶点的四边形有且仅有一个正方形.
,使得以它们为顶点的四边形有且仅有一个正方形.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{π}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{16}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com