
分析 由题意建立直角坐标系,边长为2的菱形ABCD中,∠BAD=60°,可得A(-$\sqrt{3}$,0),B(0,1),D(0,-1).利用向量的坐标运算和数量积运算可得$\overrightarrow{DE}、\overrightarrow{BF}$,再利用二次函数的单调性可得$\overrightarrow{DE}$•$\overrightarrow{BF}$的最大值.
解答 解:如图所示,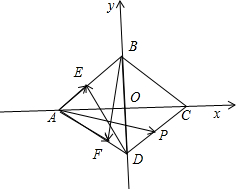
∵边长为2的菱形ABCD中,∠BAD=60°,
∴A(-$\sqrt{3}$,0),B(0,1),D(0,-1).
∴$\overrightarrow{AB}$=($\sqrt{3}$,1),$\overrightarrow{AD}$=($\sqrt{3}$,-1).
$\overrightarrow{DE}$=$(\overrightarrow{AE}-\overrightarrow{AD})$=λ$\overrightarrow{AB}$-$\overrightarrow{AD}$=($\sqrt{3}λ-\sqrt{3}$,λ+1),(0≤λ≤1).
$\overrightarrow{BF}$=$\overrightarrow{AF}-\overrightarrow{AB}$=(1-λ)$\overrightarrow{AD}$-$\overrightarrow{AB}$=(-$\sqrt{3}$λ,λ-2).
∴$\overrightarrow{DE}$•$\overrightarrow{BF}$=-$\sqrt{3}$λ($\sqrt{3}$λ-$\sqrt{3}$)+(λ+1)(λ-2)=-2λ2+2λ-2
=-2$(λ-\frac{1}{2})^{2}-\frac{3}{2}$,∵0≤λ≤1,
∴当λ=$\frac{1}{2}$时,$\overrightarrow{DE}$•$\overrightarrow{BF}$的最大值为-$\frac{3}{2}$.
故答案为:$-\frac{3}{2}$.
点评 本题考查了向量的坐标运算和数量积运算、二次函数的单调性,考查了推理能力和计算能力,属于中档题.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:解答题
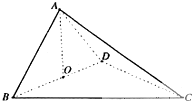 如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,AB=2,AC=$\sqrt{6}$.
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,AB=2,AC=$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com