
【题目】如图,已知顶点![]() ,
,![]() ,动点
,动点![]() 分别在
分别在![]() 轴,
轴,![]() 轴上移动,延长
轴上移动,延长![]() 至点
至点![]() ,使得
,使得![]() ,且
,且![]() .
.
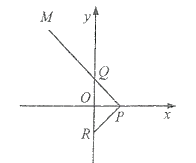
(1)求动点![]() 的轨迹
的轨迹![]() ;
;
(2)过点![]() 分别作直线
分别作直线![]() 交曲线于
交曲线于![]() 两点,若直线
两点,若直线![]() 的倾斜角互补,证明:直线的斜率为定值;
的倾斜角互补,证明:直线的斜率为定值;
(3)过点![]() 分别作直线
分别作直线![]() 交曲线于
交曲线于![]() 两点,若
两点,若![]() ,直线
,直线![]() 是否经过定点?若是,求出该定点,若不是,说明理由.
是否经过定点?若是,求出该定点,若不是,说明理由.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)设点M,P,Q的坐标,将向量进行坐标化,整理即可得轨迹方程;(2)设点![]() ,
,![]() ,直线
,直线![]() 的倾斜角互补,则两直线斜率互为相反数,用斜率公式计算得到
的倾斜角互补,则两直线斜率互为相反数,用斜率公式计算得到![]() ,即可计算kAB;(3)若
,即可计算kAB;(3)若![]() ,由两直线斜率积为-1,可得到关于
,由两直线斜率积为-1,可得到关于![]() 与
与![]() 的等量关系,写出直线AB 的方程,将等量关系代入直线方程整理可得直线AB经过的定点.
的等量关系,写出直线AB 的方程,将等量关系代入直线方程整理可得直线AB经过的定点.
(1)设![]() ,
,![]() ,
,![]() .
.
由![]() ,得
,得![]() ,即
,即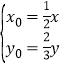 .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
所以动点![]() 的轨迹为抛物线
的轨迹为抛物线![]() ,其方程为
,其方程为![]() .
.
(2)证明:设点![]() ,
,![]() ,
,
若直线![]() 的倾斜角互补,则两直线斜率互为相反数,
的倾斜角互补,则两直线斜率互为相反数,
又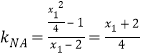 ,
,![]() ,所以
,所以![]() ,
,
![]() ,整理得
,整理得![]() ,
,
所以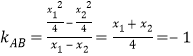 .
.
(3)因为![]() ,
,
所以![]() ,
,
即![]() ,①
,①
直线![]() 的方程为:
的方程为:![]() ,
,
整理得:![]() ,②
,②
将①代入②得![]() ,即
,即![]() ,
,
当![]() 时
时![]() ,
,
即直线![]() 经过定点
经过定点![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=2,a2=4,且当n≥2时,an2=an-1an+1,![]() ;
;
(1)求数列{an}的通项公式an;
(2)若bn=(2n-1)an,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |
(I)在答题卡上作出这些数据的频率分布直方图:
(II)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查教师对教育改革认识水平,现从某市年龄在![]() 的教师队伍中随机选取100名教师,得到的频率分布直方图如图所示,若从年龄在
的教师队伍中随机选取100名教师,得到的频率分布直方图如图所示,若从年龄在![]() 中用分层抽样的方法选取6名教师代表.
中用分层抽样的方法选取6名教师代表.

(1)求年龄在![]() 中的教师代表人数;
中的教师代表人数;
(2)在这6名教师代表中随机选取2名教师,求在![]() 中至少有一名教师被选中的概率.
中至少有一名教师被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是各项均不为
是各项均不为![]() 的等差数列,公差为
的等差数列,公差为![]() ,
,![]() 为其前
为其前![]() 项和,且满足
项和,且满足
![]() ,
,![]() .数列
.数列![]() 满足
满足![]() ,
,![]() 为数列
为数列![]() 的前n项和.
的前n项和.
(1)求![]() 、
、![]() 和
和![]() ;
;
(2)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=![]() ,DE=3,∠BAD=60°,G为BC的中点,H为CD中点.
,DE=3,∠BAD=60°,G为BC的中点,H为CD中点.
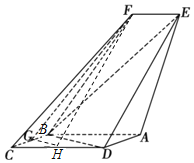
(1)求证:平面FGH∥平面BED;
(2)求证:BD⊥平面AED;
(3)求直线EF与平面BED所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某工厂要设计一个部件(如图阴影部分所示),要求从圆形铁片上进行裁剪,部件由三个全等的矩形和一个等边三角形构成,设矩形的两边长分别为![]() ,
,![]() (单位:cm),且要求
(单位:cm),且要求![]() ,部件的面积是
,部件的面积是![]() .
.

(1)求y关于x的函数表达式,并求定义域;
(2)为了节省材料,请问x取何值时,所用到的圆形铁片面积最小,并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,过椭圆的左焦点
,过椭圆的左焦点![]() 且倾斜角为
且倾斜角为![]() 的直线与圆
的直线与圆![]() 相交所得弦长为
相交所得弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,若存在,求直线
,若存在,求直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com