
已知函数f(x)=ax3+3x2-x+1在R上是减函数,求a的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
某人用10万元买了一辆小汽车用来跑出租,已知这辆汽车从启用的第一年起连续使用,第n年的保养维修费为2 000(n-1)元,使用它直到“报废最合算”(所谓“报废最合算”是指使用的这辆汽车的年平均耗资最少)为止,则最佳报废时间为________年.
查看答案和解析>>
科目:高中数学 来源: 题型:
设D是函数y=f(x)定义域内的一个区间,若存在x0∈D,使f(x0)=-x0,则称x0是f(x)的一个“次不动点”.若函数f(x)=ax2-3x-a+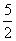 在区间[1,4]上存在次不动点,则实数a的取值范围是( )
在区间[1,4]上存在次不动点,则实数a的取值范围是( )
A.(-∞,0) B.(0, )
)
C.[ ,+∞) D.(-∞,
,+∞) D.(-∞, ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
做一个圆柱形锅炉,容积为V,两个底面的材料每单位面积的价格为a元,侧面的材料每单位面积的价格为b元,当造价最低时,锅炉的底面直径与高的比为( )
A.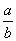 B.
B.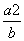 C.
C.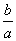 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
某单位用木料制作如图所示的框架,框架的下部是边长分别为x、y(单位:m)的矩形,上部是等腰直角三角形,要求框架围成的总面积为8m2,问x、y分别为多少时用料最省?(精确到0.001m) 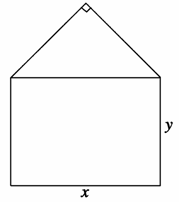
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com