
分析 (1)利用函数定义取到R的奇函数的性质:f(0)=0求解实数a的值.
(2)利用定义法证明其单调性.
(3)利用(2)函数的单调性,将不等式f(t2+2)+f(t2-tk)>0恒成立等价变换后求解实数k的取值范围.
解答 解:(1)由题意:∵函数f(x)=a-$\frac{2}{{2}^{x}+1}$是定义域为R的奇函数,
∴f(0)=0,即$a-\frac{2}{{2}^{0}-1}=0$,
解得:a=1.
当a=1时,f(x)=1-$\frac{2}{{2}^{x}+1}$=$\frac{{2}^{x}-1}{{2}^{x}+1}$
f(-x)═$\frac{{2}^{-x}-1}{{2}^{-x}+1}$=$\frac{1-{2}^{x}}{{2}^{x}+1}$=-$\frac{{2}^{x}-1}{{2}^{x}+1}$=-f(x),∴f(x)是奇函数.
故得a=1满足题意.
所以:a=1.
(2)由(1)可知f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$;
设x1<x2,那么:f(x1)-f(x2)=$\frac{{2}^{{x}_{1}}-1}{{2}^{{x}_{1}}+1}$-$\frac{{2}^{{x}_{2}}-1}{{2}^{{x}_{2}}+1}$=$\frac{2({2}^{{x}_{1}}-{2}^{{x}_{2}})}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$
∵x1<x2,
∴${2}^{{x}_{1}}-{2}^{{x}_{2}}<0$
所以:f(x1)-f(x2)<0;
故,函数f(x)为R上的增函数.
(3)由(2)知:函数f(x)为R上的增函数,且f(x)是奇函数.
从而不等式:f(t2+2)+f(t2-tk)>0等价于f(t2+2)>f(-t2+tk),即得:t2+2>-t2+tk.
∴2t2-tk+2>0对任意于t∈[-1,$\frac{1}{2}$],恒成立.
记g(t)=2t2-tk+2,开口向上,对称轴x=$\frac{k}{4}$,则g(t)在∈[-1,$\frac{1}{2}$]上的最小值大于0.即恒成立.
①当$\frac{k}{4}$<-1时,即k<-4时,g(t)=2t2-tk+2在[-1,$\frac{1}{2}$]上是单调增函数,
g(t)min=g(-1)=4+k>0,解得:k>-4,
故得k无解,
②当-1≤$\frac{k}{4}$$≤\frac{1}{2}$时,即-4≤k≤2时,g(t)min=g($\frac{k}{4}$)=2-$\frac{{k}^{2}}{8}$>0,解得:4>k>-4,
故得-4<k≤2.
③当$\frac{k}{4}$>$\frac{1}{2}$时,即k>2时,g(t)=2t2-tk+2在[-1,$\frac{1}{2}$]上是单调减函数,
g(t)min=g($\frac{1}{2}$)=$\frac{5-k}{2}$>0,解得:k<5,
故得2<k<5,
综上所述:实数k的取值范围是{k|-4<k<5}.
点评 本题考查了函数的性质之奇函数的运用,单调性的证明以及恒等式的问题的转化为二次函数最值的讨论.属于难题.


科目:高中数学 来源: 题型:选择题
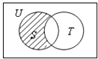
| A. | {2,4} | B. | {7,9} | C. | {1,3,5} | D. | {1,2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{x-y}$-$\frac{1}{y}$>0 | B. | 2x-3y>0 | C. | ($\frac{1}{2}$)x-($\frac{1}{2}$)y-x<0 | D. | lnx+lny>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4030 | B. | 4028 | C. | 4032 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-2)>f(1) | B. | f(-2)<f(1) | C. | f(2)=f(1) | D. | f(-2)>f(-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 作y=sin(2x+$\frac{π}{3}$)x∈[$\frac{π}{12}$,$\frac{4π}{3}$]的图象,要求:
作y=sin(2x+$\frac{π}{3}$)x∈[$\frac{π}{12}$,$\frac{4π}{3}$]的图象,要求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com