
【题目】已知平行四边形![]() 的三个顶点坐标为
的三个顶点坐标为![]() ,
,![]() ,
,![]() .
.
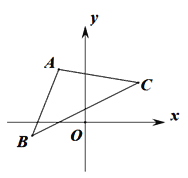
(1)求平行四边形![]() 的顶点D的坐标;
的顶点D的坐标;
(2)在![]() 中,求
中,求![]() 边上的高所在直线方程;
边上的高所在直线方程;
(3)求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)设AC的中点为M,则由M为AC的中点求得![]() ,设点D坐标为
,设点D坐标为![]() ,由已知得M为线段BD中点,求得D的坐标;
,由已知得M为线段BD中点,求得D的坐标;
(2)求得直线CD的斜率![]() ,可得CD边上的高线所在直线的斜率为
,可得CD边上的高线所在直线的斜率为![]() ,从而在
,从而在![]() 中,求得CD边上的高所在直线的方程;
中,求得CD边上的高所在直线的方程;
(3)求得![]() ,用两点式求得直线CD的方程,利用点到直线的距离公式求得点A到直线CD的距离,可得
,用两点式求得直线CD的方程,利用点到直线的距离公式求得点A到直线CD的距离,可得![]() 的面积.
的面积.
(1)由于平行四边形ABCD的三个顶点的坐标为![]() ,
,![]() ,
,![]() ,
,
设AC的中点为M,则![]() ,
,
设点D为![]() ,由已知得M为线段BD中点,有
,由已知得M为线段BD中点,有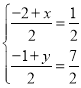 ,
,
解得![]() ,所以,
,所以,![]() ;
;
(2)![]() 直线CD的斜率
直线CD的斜率![]() ,所以CD边上的高所在直线的斜率为
,所以CD边上的高所在直线的斜率为![]() ,
,
故![]() 中,CD边上的高所在直线的方程为
中,CD边上的高所在直线的方程为![]() ,即为
,即为![]() ;
;
(3)![]() ,
,![]() ,
,![]() ,
,
由C,D两点得直线CD的方程为:![]() ,
,
![]() 点A到直线CD的距离为
点A到直线CD的距离为![]() ,
,![]() .
.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,设底面ABCD是边长为1的正方形,PA⊥面ABCD. 
(1)求证:PC⊥BD;
(2)过BD且与直线PC垂直的平面与PC交于点E,当三棱锥E﹣BCD的体积最大时,求二面角E﹣BD﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() .若对任意的
.若对任意的![]() ,
,![]() ,都有
,都有![]() .
.
(1)判断函数![]() 的单调性,并说明理由;
的单调性,并说明理由;
(2)若![]() ,求实数
,求实数![]() 的取值范围;.
的取值范围;.
(3)若不等式![]() 对任意
对任意![]() 和
和![]() 都恒成立,求实数
都恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)为二次函数,且f(x-1)+f(x)=2x2+4.
(1)求f(x)的解析式;
(2)当x∈[t,t+2],t∈R时,求函数f(x)的最小值(用t表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 市某机构为了调查该市市民对我国申办
市某机构为了调查该市市民对我国申办![]() 年足球世界杯的态度,随机选取了
年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 |
| ||
女性市民 |
| ||
合计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
(i)能否在犯错误的概率不超过![]() 的前提下认为支持申办足球世界杯与性别有关;
的前提下认为支持申办足球世界杯与性别有关;
(ii)已知在被调查的支持申办足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教师,现从这
位是教师,现从这![]() 位退休老人中随机抽取
位退休老人中随机抽取![]() 人,求至多有
人,求至多有![]() 位老师的概率.
位老师的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a3是a2与a6的等比中项,2a1+3a2=16.
(1)求数列{an}的通项公式;
(2)设bn=log2a1+log2a2+…+log2an , 求数列{ ![]() }的前n项和Sn .
}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过市场调查,超市中的某种小商品在过去的近40天的日销售量(单位:件)与价格(单位:元)为时间![]() (单位:天)的函数,且日销售量近似满足
(单位:天)的函数,且日销售量近似满足![]() ,价格近似满足
,价格近似满足![]() 。
。
(1)写出该商品的日销售额![]() (单位:元)与时间
(单位:元)与时间![]() (
(![]() )的函数解析式并用分段函数形式表示该解析式(日销售额=销售量
)的函数解析式并用分段函数形式表示该解析式(日销售额=销售量![]() 商品价格);
商品价格);
(2)求该种商品的日销售额![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】执行如图所示的程序框图,若输出的结果为2,则输入的正整数a的可能取值的集合是( ) 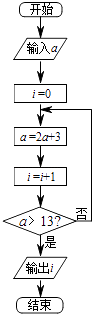
A.{1,2,3,4,5}
B.{1,2,3,4,5,6}
C.{2,3,4,5}
D.{2,3,4,5,6}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com