
 如图,已知圆M:(x-3)2+(y-3)2=4,六边形ABCDEF为圆M的内接正六边形,N为AB的中点,当正六边形ABCDEF绕圆心M转动时,$\overrightarrow{MN}•\overrightarrow{OC}$的最大值是3$\sqrt{6}$.
如图,已知圆M:(x-3)2+(y-3)2=4,六边形ABCDEF为圆M的内接正六边形,N为AB的中点,当正六边形ABCDEF绕圆心M转动时,$\overrightarrow{MN}•\overrightarrow{OC}$的最大值是3$\sqrt{6}$. 分析 运用向量的三角形法则,结合向量的数量积的定义及几何意义,$\overrightarrow{MN}$•$\overrightarrow{MC}$=0,再由向量的数量积定义及余弦函数的值域即可得到最大值.
解答 解:由题意可得$\overrightarrow{OC}$=$\overrightarrow{OM}$+$\overrightarrow{MC}$,
∴$\overrightarrow{MN}•\overrightarrow{OC}$=$\overrightarrow{MN}$•($\overrightarrow{OM}$+$\overrightarrow{MC}$)=$\overrightarrow{MN}$•$\overrightarrow{OM}$+$\overrightarrow{MN}$•$\overrightarrow{MC}$,
∵$\overrightarrow{MN}$•$\overrightarrow{MC}$=|$\overrightarrow{MN}$|•|$\overrightarrow{MC}$|cos∠NMC=$\sqrt{3}$×2×cos90°=0,
由于圆M:(x-3)2+(y-3)2=4,则圆心M(3,3),半径r=2,
则OM=3$\sqrt{2}$,MN=$\sqrt{3}$,
∴$\overrightarrow{MN}$•$\overrightarrow{OM}$=-$\overrightarrow{MN}$•$\overrightarrow{MO}$=-3$\sqrt{2}$×$\sqrt{3}$cos<$\overrightarrow{MN}$,$\overrightarrow{MO}$>∈[-3$\sqrt{6}$,3$\sqrt{6}$],
∴($\overrightarrow{MN}•\overrightarrow{OC}$)max=3$\sqrt{6}$.
故答案为:3$\sqrt{6}$
点评 本题主要考查两个向量的数量积的定义,两个向量的加减法的法则,以及其几何意义,余弦函数的值域,属于中档题.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
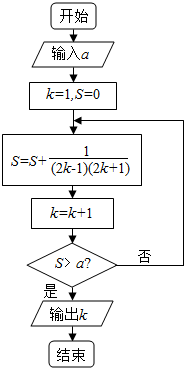 已知函数f(x)=$\left\{\begin{array}{l}{\frac{{x}^{2}}{19},x>2}\\{f(x+1),x≤2}\end{array}\right.$,阅读如图所示的程序框图,若输入a的值为f(1)的值,则输出的k值是( )
已知函数f(x)=$\left\{\begin{array}{l}{\frac{{x}^{2}}{19},x>2}\\{f(x+1),x≤2}\end{array}\right.$,阅读如图所示的程序框图,若输入a的值为f(1)的值,则输出的k值是( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 35 | B. | 36 | C. | 120 | D. | 121 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com