
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
分析 棱柱为直棱柱,底面为直角三角形,故而球心位于侧面BCC1B1的中心,根据球的半径计算棱柱的高即可求出棱柱的体积.
解答 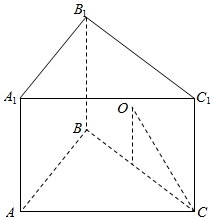 解:∵AB=AC=1,BC=$\sqrt{2}$
解:∵AB=AC=1,BC=$\sqrt{2}$
∴AB⊥AC,
∵CC1⊥平面ABC,三棱柱ABC-A1B1C1内接于球O,
∴O为矩形BCC1B1的中心,
设球O半径为r,则4πr2=3π,∴r=$\frac{\sqrt{3}}{2}$.
即OC=r=$\frac{\sqrt{3}}{2}$,
∴三棱柱的高h=2$\sqrt{{r}^{2}-(\frac{1}{2}BC)^{2}}$=1.
∴三棱柱的体积V=S△ABC•h=$\frac{1}{2}×1×1×1$=$\frac{1}{2}$.
故选C.
点评 本题考查了棱柱与外接球的关系,棱柱的体积计算,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
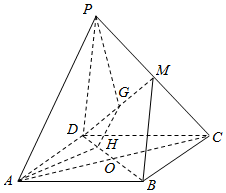 如图,P是菱形ABCD所在平面外一点,∠BAD=60°,△PCD是等边三角形,AB=2,PA=2$\sqrt{2}$,M是PC的中点,点G为线段DM上一点(端点除外),平面APG与BD交于点H.
如图,P是菱形ABCD所在平面外一点,∠BAD=60°,△PCD是等边三角形,AB=2,PA=2$\sqrt{2}$,M是PC的中点,点G为线段DM上一点(端点除外),平面APG与BD交于点H.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
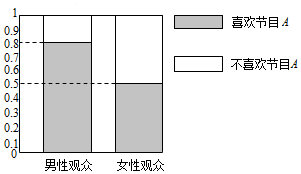 某媒体为调查喜欢娱乐节目A是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
某媒体为调查喜欢娱乐节目A是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:| 喜欢节目A | 不喜欢节目A | 总计 | |
| 男性观众 | 24 | 6 | 30 |
| 女性观众 | 15 | 15 | 30 |
| 总计 | 39 | 21 | 60 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
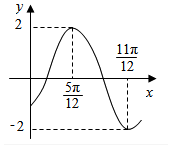
| A. | $-\frac{3}{2}$ | B. | -1 | C. | $-\sqrt{2}$ | D. | $-\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com