
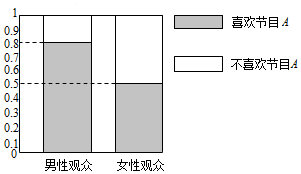
 某媒体为调查喜欢娱乐节目A是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
某媒体为调查喜欢娱乐节目A是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:| 喜欢节目A | 不喜欢节目A | 总计 | |
| 男性观众 | 24 | 6 | 30 |
| 女性观众 | 15 | 15 | 30 |
| 总计 | 39 | 21 | 60 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
分析 (Ⅰ)由题意和条形图易得列联表,计算可得则K2的观测值k≈5.934>3.841,可得有关;
(Ⅱ)利用分层抽样在男性观众30名中抽取5名,其中喜欢娱乐节目A的人数为4,记为a,b,c,d,不喜欢节目A的人数为1,记为1,列举可得总的方法种数,找出符合题意的方法种数,由概率公式可得.
解答 解:(Ⅰ)由题意得列联表如下:
| 喜欢节目A | 不喜欢节目A | 总计 | |
| 男性观众 | 24 | 6 | 30 |
| 女性观众 | 15 | 15 | 30 |
| 总计 | 39 | 21 | 60 |
点评 本题考查独立检验,涉及列举法求古典概型的概率,属基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
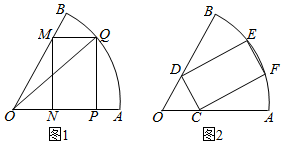 如图,在中心角为60°,半径为1的扇形OAB的半径OB上任取一点M,作内接矩形MNPQ,设∠QOA=θ,矩形MNPQ的面积为S.
如图,在中心角为60°,半径为1的扇形OAB的半径OB上任取一点M,作内接矩形MNPQ,设∠QOA=θ,矩形MNPQ的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-∞,1) | C. | (-1,0)∪(0,3) | D. | (-∞,0)∪(0,1) |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年山西忻州一中高一上学期新生摸底数学试卷(解析版) 题型:解答题
如图,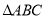 和
和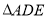 是有公共顶点的等腰直角三角形,
是有公共顶点的等腰直角三角形, ,点
,点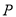 为射线
为射线 与射线
与射线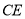 的交点.
的交点.
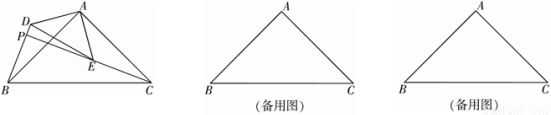
(1)求证: ;
;
(2)若 ,把
,把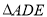 绕点
绕点 旋转,
旋转,
①当 时,求
时,求 的长;
的长;
②直接写出旋转过程中线段 长的最小值与最大值.
长的最小值与最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com