
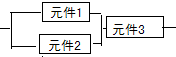
 某一部件由三个电子元件按如图所示方式连接而成,元件1或元件2正常工作,则部件正常工作:设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,σ2),若每个元件使用寿命超过1200小时的概率为
某一部件由三个电子元件按如图所示方式连接而成,元件1或元件2正常工作,则部件正常工作:设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,σ2),若每个元件使用寿命超过1200小时的概率为| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 16 |
| 27 |
| 16 |
| 27 |


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
| x2 |
| 2 |
| OM |
| ON |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| sin(x+π) |
| cos(π-x) |
| A、f(x)的最小正周期是2π | ||
| B、f(x)在[4,5]上单调递增 | ||
C、f(x)的图象关于x=
| ||
D、f(x)的图象关于点(
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com