
分析 (1)由正弦定理可知a-b=bcosC,则sinA-sinB=sinBcosC,由A=π-(B+C),根据诱导公式及两角和的正弦公式,即可求得sinC=tanB;
(2)由题意求得$cosC=-\frac{1}{2}$,利用余弦定理即可求得c的值.
解答 解:(1)由正弦定理可知:$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R,则a=2RsinA,b=2RsinB,c=2RsinC,
由a-b=bcosC,则sinA-sinB=sinBcosC,
由A=π-(B+C),则sinA=sin[π-(B+C)]=sin(B+C),
即sin(B+C)=sinB+sinBcosC,sinBcosC+cosBsinC=sinB+sinBcosC,
sinCcosB=sinB,tanB=$\frac{sinB}{cosB}$,
∴sinC=tanB.
(Ⅱ)由a-b=bcosC,且a=1,b=2,得$cosC=-\frac{1}{2}$,
由余弦定理,${c^2}={a^2}+{b^2}-2abcosC=1+4-2×1×2×({-\frac{1}{2}})=7$,
∴$c=\sqrt{7}$,
c的值为$\sqrt{7}$.
点评 本题考查正弦定理及余弦定理的应用,两角和的正弦公式,考查计算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间 | (0,2) | [2,4) | [4,6) | [6,8) | 8小时以上 |
| 男生人数 | 10 | 25 | 35 | 30 | x |
| 女生人数 | 15 | 30 | 25 | y | 5 |
| 男生 | 女生 | 总计 | |
| 平均时间不超过6小时 | |||
| 平均时间超过6小时 | |||
| 总计 |
| K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$ | P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 6.635 | 7.789 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相交 | B. | 内切 | C. | 外切 | D. | 相离 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
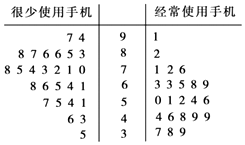 当今信息时代,众多中小学生也配上了手机.某机构为研究经常使用手机是否对学习成绩有影响,在某校高三年级50名理科生第人的10次数学考成绩中随机抽取一次成绩,用茎叶图表示如图:
当今信息时代,众多中小学生也配上了手机.某机构为研究经常使用手机是否对学习成绩有影响,在某校高三年级50名理科生第人的10次数学考成绩中随机抽取一次成绩,用茎叶图表示如图:| 及格(60及60以上) | 不及格 | 合计 | |
| 很少使用手机 | 20 | 7 | 27 |
| 经常使用手机 | 10 | 13 | 23 |
| 合计 | 30 | 20 | 50 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 |
| k0 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{4}$)∪(2$\sqrt{3}$-2,$\frac{3}{2}$] | B. | [0,$\frac{1}{4}$)∪(2$\sqrt{3}$-2,$\frac{3}{2}$] | C. | [0,$\frac{1}{4}$]∪(2$\sqrt{3}$-2,$\frac{3}{2}$] | D. | (0,$\frac{1}{4}$]∪(2$\sqrt{3}$-2,$\frac{3}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com