考点:数列的求和,等比数列的通项公式,等比数列的前n项和,等差数列的性质
专题:计算题,等差数列与等比数列
分析:(Ⅰ)根据a2,a1+a3,a4成等差数列得到2(a1+a3)=a2+a4,应用等比数列通项公式,化简求出公比,写出通项an;
(Ⅱ)运用分组求和求出Sn,注意分成两组都是等比数列,并运用等比数列求和公式,然后求出bn,并对bn拆成两项的差,运用裂项相消求和即可求出Tn.
解答:
解:(Ⅰ)设等比数列的公比为q,由已知得:2(a
1+a
3)=a
2+a
4,
即2(a
1+a
1q
2)=a
1q+a
1q
3,解得q=2,
又∵a
1=2,
∴a
n=a
1q
n-1=2
n;
(Ⅱ)由(Ⅰ)得:
S
n=(a
12+a
22+a
32+…+a
n2)-(a
1+a
2+…+a
n)
=(4+4
2+4
3+…+4
n)-(2+2
2+2
3+…+2
n)
=
-
=
(4
n-1)-2(2
n-1)=(2
n-1)(
•2
n-
)=
(2
n-1)(2
n+1-1),
又b
n=
,
∴b
n=
•=
(
-),
∴T
n=b
1+b
2+b
3+…+b
n-1+b
n=
[(
-)+(
-)+(
-)+…+(
-)
+(
-)]
=
(1-
)=
-
.
点评:本题主要考查等比数列的通项公式与求和公式,以及等差数列的性质,考查两种数列求和方法:分组求和与裂项相消求和,这是两种重要的求和方法,务必掌握.



 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案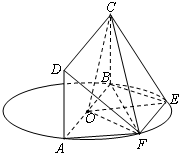 如图,AB为圆O的直径,点E、F在圆O上,矩形ABCD所在平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
如图,AB为圆O的直径,点E、F在圆O上,矩形ABCD所在平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.