
【题目】如图,多面体![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,四边形
,四边形![]() 是菱形.
是菱形.
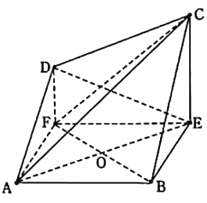
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,设
,设![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某大型商场为了了解顾客的购物信息,随机在商场收集了![]() 位顾客的购物总额(单位元),将数据按照
位顾客的购物总额(单位元),将数据按照![]()
![]() ,
,![]()
![]() 分成
分成![]() 组,制成了如下图所示的频率分布直方图:
组,制成了如下图所示的频率分布直方图:
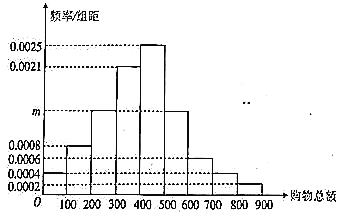
该商场每日大约有![]() 名顾客,为了增加商场销售总额,近期对一次性购物不低于
名顾客,为了增加商场销售总额,近期对一次性购物不低于![]() 元的顾客发放纪念品.
元的顾客发放纪念品.
(1)求频率分布直方图中![]() 的值,并估计每日应准备纪念品的数量;
的值,并估计每日应准备纪念品的数量;
(2)若每日按分层抽样的方法从购物总额在![]() 三组对应的顾客中抽取
三组对应的顾客中抽取![]() 名顾客,这
名顾客,这![]() 名顾客中再随机抽取两名超级顾客,每人奖励一个超级礼包,求获得超级礼包的两人来自不同组的概率.
名顾客中再随机抽取两名超级顾客,每人奖励一个超级礼包,求获得超级礼包的两人来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学为调查来自南方和北方的同龄大学生的身高差异,从2016级的年龄在18~19岁之间的大学生中随机抽取了来自南方和北方的大学生各10名,测量他们的身高,量出的身高如下(单位:cm):
南方:158,170,166,169,180,175,171,176,162,163.
北方:183,173,169,163,179,171,157,175,184,166.
(1)根据抽测结果,画出茎叶图,对来自南方和北方的大学生的身高作比较,写出统计结论.
(2)设抽测的10名南方大学生的平均身高为![]() cm,将10名南方大学生的身高依次输入如图所示的程序框图进行运算,问输出的s大小为多少?并说明s的统计学意义。
cm,将10名南方大学生的身高依次输入如图所示的程序框图进行运算,问输出的s大小为多少?并说明s的统计学意义。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() (其中
(其中![]() )的部分图象如图所示,把函数
)的部分图象如图所示,把函数![]() 的图像向右平移
的图像向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位,得到函数
个单位,得到函数![]() 的图像。
的图像。

(1)当![]() 时,若方程
时,若方程![]() 恰好有两个不同的根
恰好有两个不同的根![]() ,求
,求![]() 的取值范围及
的取值范围及![]() 的值;
的值;
(2)令![]() ,若对任意
,若对任意![]() 都有
都有![]() 恒成立,求
恒成立,求![]() 的最大值
的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产的产品在出厂前都要做质量检测,每件一等品都能通过检测,每件二等品通过检测的概率为![]() .现有
.现有![]() 件产品,其中
件产品,其中![]() 件是一等品,
件是一等品, ![]() 件是二等品.
件是二等品.
(Ⅰ)随机选取![]() 件产品,设至少有一件通过检测为事件
件产品,设至少有一件通过检测为事件![]() ,求事件
,求事件![]() 的概率;
的概率;
(Ⅱ)随机选取![]() 件产品,其中一等品的件数记为
件产品,其中一等品的件数记为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“双十一网购狂欢节”源于淘宝商城(天猫)2009年11月11 日举办的促销活动,当时参与的商家数量和促销力度均有限,但营业额远超预想的效果,于是11月11日成为天猫举办大规模促销活动的固定日期.如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商分析近8年“双十一”期间的宣传费用![]() (单位:万元)和利润
(单位:万元)和利润![]() (单位:十万元)之间的关系,得到下列数据:
(单位:十万元)之间的关系,得到下列数据:
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(1)请用相关系数![]() 说明
说明![]() 与
与![]() 之间是否存在线性相关关系(当
之间是否存在线性相关关系(当![]() 时,说明
时,说明![]() 与
与![]() 之间具有线性相关关系);
之间具有线性相关关系);
(2)根据(1)的判断结果,建立![]() 与
与![]() 之间的回归方程,并预测当
之间的回归方程,并预测当![]() 时,对应的利润
时,对应的利润![]() 为多少(
为多少(![]() 精确到0.1).
精确到0.1).
附参考公式:回归方程中![]() 中
中![]() 和
和![]() 最小二乘估计分别为
最小二乘估计分别为
 ,相关系数
,相关系数
参考数据:
 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线过点
,直线过点![]() ,且
,且![]() ,线段
,线段![]() 交圆
交圆![]() 的交点为点
的交点为点![]() ,
,![]() 是
是![]() 关于轴的对称点.
关于轴的对称点.
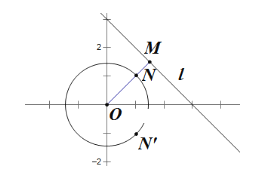
(1)求直线![]() 的方程;
的方程;
(2)已知![]() 是圆
是圆![]() 上不同的两点,且
上不同的两点,且![]() ,试证明直线
,试证明直线![]() 的斜率为定值,并求出该定值.
的斜率为定值,并求出该定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com