Question

18．如图所示，某几何体的三视图相同，均为圆周的$\frac{1}{4}$，则该几何体的表面积为（　　）

• A． $\frac{3}{4}$π
• B． $\frac{5}{4}$π
• C． π
• D． 2π

Answer 1

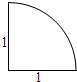
分析 根据三视图得出可以判断几何体是半径为1的球的$\frac{1}{8}$．运用数据得出该几何体的表面积为3×$\frac{1}{4}$×π×1²+$\frac{1}{8}$×4×π×1²=$\frac{5}{4}$π，

解答 解：∵某几何体的三视图相同，均为圆周的$\frac{1}{4}$，
∴可以判断几何体是半径为1的球的$\frac{1}{8}$．

∴该几何体的表面积为3×$\frac{1}{4}$×π×1²+$\frac{1}{8}$×4×π×1²=$\frac{5}{4}$π，
故选：B

点评 本题考查了由三视图求几何体的表面积，根据三视图判断几何体的形状及数据所对应的几何量是解题的关键，属于中档题．