

分析 (1)先求出样本容量,再求出对应的平均数,根据数据补充完整条形统计图;
(2)求出只有2名留守儿童的班级个数,用树状图求出基本事件数,计算所求的概率.
解答 解:(1)根据题意,得;
该校班级个数为4÷20%=20(个),
只有2名留守儿童的班级个数为:
20-(2+3+4+5+4)=2(个),
该校平均每班留守儿童的人数为:
$\frac{1×2+2×2+3×3+4×4+5×5+6×4}{20}$=4(名),--------(2分)
条形统计图补充如下: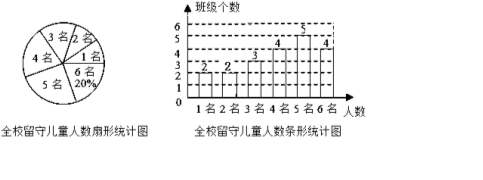
----------(4分)
(2)由(1)得只有2名留守儿童的班级有2个,共4名学生,
设A1,A2来自一个班,B1,B2来自一个班,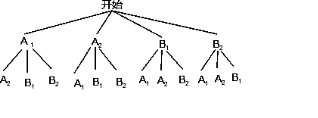
画出树状图如图所示,----------(6分)
由树状图知,共有12种可能的情况,并且每种结果出现的可能性相等,
其中来自一个班的共有4种情况,
则所选两名留守儿童来自同一个班级的概率为:P=$\frac{4}{12}$=$\frac{1}{3}$.----------(8分)
点评 本题考查了频率分布直方图的应用问题,也考查了用列举法求古典概型的概率的应用问题,是基础题目.


科目:高中数学 来源: 题型:填空题
 如图,三个半径都是5cm的小球放在一个半球面的碗中,三个小球的顶端恰好与碗的上沿处于同一水平面,则这个碗的半径R是5$+\frac{5\sqrt{21}}{3}$cm.
如图,三个半径都是5cm的小球放在一个半球面的碗中,三个小球的顶端恰好与碗的上沿处于同一水平面,则这个碗的半径R是5$+\frac{5\sqrt{21}}{3}$cm.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$ | B. | -$\frac{7}{2}$ | C. | -2 | D. | -$\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
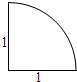
| A. | $\frac{3}{4}$π | B. | $\frac{5}{4}$π | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sinA)>f(sinB) | B. | f(cosA)>f(cosB) | C. | f(sinA)>f(cosB) | D. | f(cosA)>f(sinB) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10,-10 | B. | 20,-20 | C. | 30,20 | D. | 30,10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
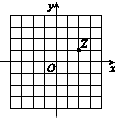 若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,则复数$\frac{z}{1-2i}$的共轭复数是( )
若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,则复数$\frac{z}{1-2i}$的共轭复数是( )| A. | -$\frac{3}{5}$i | B. | -i | C. | $\frac{3}{5}$i | D. | i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com