
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 求出A中不等式的解集,找出解集中的整数解确定出A,求出B中不等式的解集确定出B,找出A与B的交集,即可做出判断.
解答 解:由A中不等式变形得:log2x<4=log216,即0<x<16,x∈Z,
∴A={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15},
由B中不等式变形得:$\frac{5}{3-x}$-1≥0,
整理得:$\frac{2+x}{3-x}$≥0,即$\frac{x+2}{x-3}$≤0,
解得:-2≤x<3,即B=[-2,3),
∴A∩B={1,2},即A∩B的元素个数为2,
故选:A.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<c<a | C. | a<c<b | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
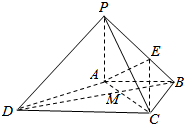 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB∥DC,AB⊥BC,且PA=AB=BC=$\frac{1}{2}$CD,BE=$\frac{1}{3}$BP.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB∥DC,AB⊥BC,且PA=AB=BC=$\frac{1}{2}$CD,BE=$\frac{1}{3}$BP.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
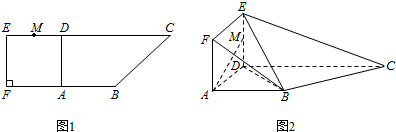
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
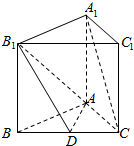 已知正三棱柱ABC-A1B1C1中,BC=1,D是棱BC上的动点.
已知正三棱柱ABC-A1B1C1中,BC=1,D是棱BC上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com