
分析 (1)通过变形$\frac{sinsinx}{x}$=$\frac{sinsinx}{sinx}$•$\frac{sinx}{x}$及换元法,利用$\underset{lim}{x→0}$$\frac{sinx}{x}$=1及极限的运算性质计算即得结论;
(2)利用洛必达法则及$\underset{lim}{x→0}$$\frac{sinx}{x}$=1计算即得结论;
(3)利用$\underset{lim}{x→0}$$(1+x)^{\frac{1}{x}}$=e计算即得结论.
解答 解:(1)$\underset{lim}{x→0}$$\frac{sinsinx}{x}$=$\underset{lim}{x→0}$($\frac{sinsinx}{sinx}$•$\frac{sinx}{x}$)
=$\underset{lim}{x→0}$$\frac{sinsinx}{sinx}$•$\underset{lim}{x→0}$$\frac{sinx}{x}$,
记t=sinx,则当x→0时t→0,
∴$\underset{lim}{x→0}$$\frac{sinsinx}{sinx}$=$\underset{lim}{t→0}$$\frac{sint}{t}$=1,
∴$\underset{lim}{x→0}$$\frac{sinsinx}{x}$=1•1=1;
(2)$\underset{lim}{x→0}$$\frac{sin4x}{\sqrt{x+1}-1}$=$\underset{lim}{x→0}$$\frac{sin4x}{\frac{1}{2}x}$
=8$\underset{lim}{x→0}$$\frac{sin4x}{4x}$
=8;
(3)$\underset{lim}{x→0}$($\frac{1+x}{1-x}$)${\;}^{\frac{1}{x}}$=$\underset{lim}{x→0}$$(\frac{1-x+2x}{1-x})^{\frac{1}{x}}$
=$\underset{lim}{x→0}$$(1+\frac{2x}{1-x})^{\frac{1-x}{2x}•\frac{2}{1-x}}$
=${e}^{\underset{lim}{x→0}\frac{2}{1-x}}$
=e2.
点评 本题考查极限及其运算,涉及两个重要极限公式、洛必达法则等基础知识,注意解题方法的积累,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (1,3] | C. | (2,3] | D. | (1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
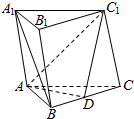 如图,正三棱柱ABC-A1B1C1的各棱均相等,AB=2,D是BC上的一点,AD⊥C1D.
如图,正三棱柱ABC-A1B1C1的各棱均相等,AB=2,D是BC上的一点,AD⊥C1D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
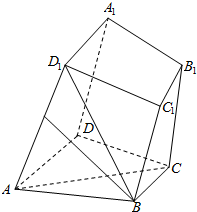 如图所示,四棱柱ABCD-A1B1C1D1中,底面ABCD是梯形,AD∥BC,侧面ABB1A1为菱形,∠DAB=∠DAA1
如图所示,四棱柱ABCD-A1B1C1D1中,底面ABCD是梯形,AD∥BC,侧面ABB1A1为菱形,∠DAB=∠DAA1查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com