
分析 设t=x2-4x+1,利用换元法结合复合函数单调性之间的关系进行求解即可.
解答 解:设t=x2-4x+1,则t=(x-2)2-3,
对称轴为x=2,
∵0<a<1,
∴y=at为减函数,
当x≥2时,函数t=x2-4x+1为增函数,
∵y=at为减函数,∴y=a${\;}^{{x}^{2}-4x+1}$为减函数,即单调递减区间为[2,+∞),
当x≤2时,函数t=x2-4x+1为减函数,
∵y=at为减函数,∴y=a${\;}^{{x}^{2}-4x+1}$为增函数,即单调递增区间为(-∞,2].
∵t=(x-2)2-3≥-3,
∴y=at≤a-3,
∵y=at>0,
∴0<y≤a-3,
即函数的值域为(0,a-3].
点评 本题主要考查函数单调性的求解,利用换元法结合复合函数单调性之间的关系是解决本题的关键.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:选择题
| A. | p是假命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | B. | p是假命题,¬p:?x0∈(0,$\frac{π}{2}$),f(x)≥0 | ||
| C. | p是真命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | D. | p是真命题,¬p:?x0∈(0,$\frac{π}{2}$),f(x)≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
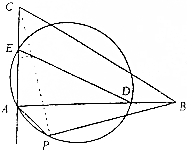 如图,△BC中,AB>AC,点D、E分别在边AB、AC上,且BD=CE,∠BAC的外角平分线与△ADE的外接圆交于A、P两点.求证:A、P、B、C四点共圆.
如图,△BC中,AB>AC,点D、E分别在边AB、AC上,且BD=CE,∠BAC的外角平分线与△ADE的外接圆交于A、P两点.求证:A、P、B、C四点共圆.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第4名学生操作了n台设备 | B. | 第4名学生操作了3台设备 | ||
| C. | 第3名学生操作了n台设备 | D. | 第3名学生操作了4台设备 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com