
ΓΨΧβΡΩΓΩΨίœΛ,2017ΡξΫΧ”ΐΜζΤς»Υ»Ϊ«ρ –≥ΓΙφΡΘ“―¥οΒΫ8.19“ΎΟά‘Σ,÷–Ιζ’ΦΨί»Ϊ«ρ –≥ΓΖίΕν10.8%.Ά®ΙΐΦρΒΞΥφΜζ≥ι―υΒΟΒΫ40Φ“÷–ΙζΜζΤς»Υ÷Τ‘λΤσ“Β,œ¬ΆΦ «40Φ“Τσ“ΒΜζΤς»ΥΒΡ≤ζ÷ΒΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ.

Θ®1Θ©«σ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®2Θ©‘Ύ…œ ω≥ι»ΓΒΡ40ΗωΤσ“Β÷–»Έ»Γ3ΗωΘ§≥ιΒΫ≤ζ÷Β–Γ”Ύ500Άρ‘ΣΒΡΤσ“Β≤Μ≥§ΙΐΝΫΗωΒΡΗ≈¬ «Εύ…ΌΘΩ
Θ®3Θ©‘Ύ…œ ω≥ι»ΓΒΡ40ΗωΤσ“Β÷–»Έ»Γ2Ηω,…η![]() ΈΣ≤ζ÷Β≤Μ≥§Ιΐ500Άρ‘ΣΒΡΤσ“ΒΗω ΐΦθ»Ξ≥§Ιΐ500Άρ‘ΣΒΡΤσ“ΒΗω ΐΒΡ≤ν÷Β,«σ
ΈΣ≤ζ÷Β≤Μ≥§Ιΐ500Άρ‘ΣΒΡΤσ“ΒΗω ΐΦθ»Ξ≥§Ιΐ500Άρ‘ΣΒΡΤσ“ΒΗω ΐΒΡ≤ν÷Β,«σ![]() ΒΡΖ÷≤ΦΝ–ΦΑΤΎΆϊ.
ΒΡΖ÷≤ΦΝ–ΦΑΤΎΆϊ.
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() ΘΜΘ®3Θ©
ΘΜΘ®3Θ©![]() .
.
ΓΨΫβΈωΓΩΖ÷ΈωΘΚΘ®1Θ©ΗυΨίΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΗςΨΊ–ΈΒΡΟφΜΐΚΆΈΣ![]() Ω…ΦΤΥψ≥ω
Ω…ΦΤΥψ≥ω![]() .
.
Θ®2Θ©ΗυΨίΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΦΤΥψ≥ω≤ζ÷Β–Γ”Ύ500Άρ‘ΣΒΡΤσ“ΒΙ≤![]() ΗωΘ§“ρ¥ΥΥυ«σΒΡΗ≈¬ ΈΣ
ΗωΘ§“ρ¥ΥΥυ«σΒΡΗ≈¬ ΈΣ![]() ΘΜ
ΘΜ
Θ®3Θ©![]() Ω…»Γ
Ω…»Γ![]() Θ§‘Υ”Ο≥§ΦΗΚΈΖ÷≤ΦΩ…“‘ΦΤΥψ
Θ§‘Υ”Ο≥§ΦΗΚΈΖ÷≤ΦΩ…“‘ΦΤΥψ![]() »ΓΗς÷ΒΒΡΗ≈¬ Θ§¥”ΕχΒΟΒΫΤδΖ÷≤ΦΝ–ΚΆΤΎΆϊ.
»ΓΗς÷ΒΒΡΗ≈¬ Θ§¥”ΕχΒΟΒΫΤδΖ÷≤ΦΝ–ΚΆΤΎΆϊ.
œξΫβΘΚΘ®1Θ©ΗυΨίΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΩ…÷ΣΘ§![]() Θ°
Θ°
≤ζ÷Β–Γ”Ύ500Άρ‘ΣΒΡΤσ“ΒΗω ΐΈΣΘΚ![]() Θ§
Θ§
Υυ“‘≥ιΒΫ≤ζ÷Β–Γ”Ύ500Άρ‘ΣΒΡΤσ“Β≤Μ≥§ΙΐΝΫΗωΒΡΗ≈¬ ΈΣ![]() Θ°
Θ°
Θ®3Θ©![]() ΒΡΥυ”–Ω…Ρή»Γ÷ΒΈΣ
ΒΡΥυ”–Ω…Ρή»Γ÷ΒΈΣ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ°
Θ°
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ°
Θ°
Γύ![]() ΒΡΖ÷≤ΦΝ–ΈΣΘΚ
ΒΡΖ÷≤ΦΝ–ΈΣΘΚ
|
|
|
|
|
|
|
|
ΤΎΆϊΈΣΘΚ![]() Θ°
Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩf(x) «Ε®“ε‘ΎR…œΒΡΤφΚ· ΐΘ§Ε‘xΘ§yΓ RΕΦ”–f(xΘΪy)ΘΫf(x)ΘΪf(y)Θ§«“Β±x>0 ±Θ§f(x)<0Θ§f(Θ≠1)ΘΫ2.
(1)«σ÷ΛΘΚf(x)ΈΣΤφΚ· ΐΘΜ
(2)«σ÷ΛΘΚf(x) «R…œΒΡΦθΚ· ΐΘΜ
(3)«σf(x)‘Ύ[Θ≠2Θ§4]…œΒΡΉν÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΙέ≤λœ¬Ν–»ΐΫ«–Έ ΐ±μΘΚ 
ΦΌ…ηΒΎn––ΒΡΒΎΕΰΗω ΐΈΣ ![]() Θ§
Θ§
Θ®1Θ©ΙιΡ…≥ωan+1”κanΒΡΙΊœΒ ΫΘ§≤Δ«σ≥ωanΒΡΆ®œνΙΪ ΫΘΜ
Θ®2Θ©…ηanbn=1Θ®nΓί2Θ©Θ§«σ÷ΛΘΚb2+b3+Γ≠+bnΘΦ2Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηfΘ®xΘ©=|x©¹1|+|x+1|Θ°
Θ®1Θ©«σfΘ®xΘ©Γήx+2ΒΡΫβΦ·ΘΜ
Θ®2Θ©»τ≤ΜΒ» ΫfΘ®xΘ©Γί ![]() Ε‘»Έ“β Β ΐaΓΌ0Κψ≥…ΝΔΘ§«σ Β ΐxΒΡ»Γ÷ΒΖΕΈßΘ°
Ε‘»Έ“β Β ΐaΓΌ0Κψ≥…ΝΔΘ§«σ Β ΐxΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() «Ε®“ε‘Ύ
«Ε®“ε‘Ύ![]() …œΒΡ≈ΦΚ· ΐΘ§«“Β±
…œΒΡ≈ΦΚ· ΐΘ§«“Β±![]() ±Θ§
±Θ§ ![]() Θ°œ÷“―Μ≠≥ωΚ· ΐ
Θ°œ÷“―Μ≠≥ωΚ· ΐ![]() ‘Ύ
‘Ύ![]() ÷αΉσ≤ύΒΡΆΦœσΘ§»γΆΦΥυ ΨΘ§≤ΔΗυΨίΆΦœσΘΚ
÷αΉσ≤ύΒΡΆΦœσΘ§»γΆΦΥυ ΨΘ§≤ΔΗυΨίΆΦœσΘΚ

Θ®1Θ©÷±Ϋ”–¥≥ωΚ· ΐ![]() Θ§
Θ§ ![]() ΒΡ‘ω«χΦδΘΜ
ΒΡ‘ω«χΦδΘΜ
Θ®2Θ©–¥≥ωΚ· ΐ![]() Θ§
Θ§ ![]() ΒΡΫβΈω ΫΘΜ
ΒΡΫβΈω ΫΘΜ
Θ®3Θ©»τΚ· ΐ![]() Θ§
Θ§ ![]() Θ§«σΚ· ΐ
Θ§«σΚ· ΐ![]() ΒΡΉν–Γ÷Β.
ΒΡΉν–Γ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐh(x)ΘΫ(m2Θ≠5mΘΪ1)xm+1ΈΣΟίΚ· ΐΘ§«“ΈΣΤφΚ· ΐΘ°
(I)«σmΒΡ÷ΒΘΜ
(II)«σΚ· ΐg(x)ΘΫh(x)ΘΪ![]() Θ§xΓ
Θ§xΓ ![]() ΒΡ÷Β”ρΘ°
ΒΡ÷Β”ρΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τDΓδ «ΤΫΟφΠΝΆβ“ΜΒψΘ§‘ρœ¬Ν–ΟϋΧβ’ΐ»ΖΒΡ «Θ® Θ©
A.ΙΐDΓδ÷ΜΡήΉς“ΜΧθ÷±œΏ”κΤΫΟφΠΝœύΫΜ
B.ΙΐDΓδΩ…ΉςΈό ΐΧθ÷±œΏ”κΤΫΟφΠΝ¥Ι÷±
C.ΙΐDΓδ÷ΜΡήΉς“ΜΧθ÷±œΏ”κΤΫΟφΠΝΤΫ––
D.ΙΐDΓδΩ…ΉςΈό ΐΧθ÷±œΏ”κΤΫΟφΠΝΤΫ––
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§«ζœΏ
÷–Θ§«ζœΏ![]() ΒΡ≤Έ ΐΖΫ≥ΧΈΣ
ΒΡ≤Έ ΐΖΫ≥ΧΈΣ![]() Θ®
Θ®![]() ΈΣ≤Έ ΐΘ§
ΈΣ≤Έ ΐΘ§![]() Θ©Θ§“‘‘≠Βψ
Θ©Θ§“‘‘≠Βψ![]() ΈΣΦΪΒψΘ§
ΈΣΦΪΒψΘ§![]() ÷αΒΡΖ«ΗΚΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ§«ζœΏ
÷αΒΡΖ«ΗΚΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ§«ζœΏ![]() ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ
ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ![]() Θ°
Θ°
Θ®1Θ©–¥≥ω«ζœΏ![]() ΒΡΤ’Ά®ΖΫ≥ΧΚΆ«ζœΏ
ΒΡΤ’Ά®ΖΫ≥ΧΚΆ«ζœΏ![]() ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘΜ
ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘΜ
Θ®2Θ©“―÷ΣΒψ![]() ««ζœΏ
««ζœΏ![]() …œ“ΜΒψΘ§»τΒψ
…œ“ΜΒψΘ§»τΒψ![]() ΒΫ«ζœΏ
ΒΫ«ζœΏ![]() ΒΡΉν–ΓΨύάκΈΣ
ΒΡΉν–ΓΨύάκΈΣ![]() Θ§«σ
Θ§«σ![]() ΒΡ÷ΒΘ°
ΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥Εΰ ÷ΫΜ“Ή –≥ΓΕ‘Ρ≥–ΆΚ≈ΒΡΕΰ ÷Τϊ≥ΒΒΡ Ι”ΟΡξ ΐ![]() Θ®
Θ®![]() Θ©”κœζ έΦέΗώ
Θ©”κœζ έΦέΗώ![]() Θ®ΒΞΈΜΘΚΆρ‘Σ/ΝΨΘ©Ϋχ––’ϊάμΘ§ΒΟΒΫ»γœ¬ΒΡΕ‘”Π ΐΨίΘΚ
Θ®ΒΞΈΜΘΚΆρ‘Σ/ΝΨΘ©Ϋχ––’ϊάμΘ§ΒΟΒΫ»γœ¬ΒΡΕ‘”Π ΐΨίΘΚ
Ι”ΟΡξ ΐ | 2 | 4 | 6 | 8 | 10 |
œζ έΦέΗώ | 16 | 13 | 9.5 | 7 | 4.5 |
Θ®IΘ© ‘«σ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΜΊΙι÷±œΏΖΫ≥Χ
ΒΡΜΊΙι÷±œΏΖΫ≥Χ![]() .
.
Θ®≤ΈΩΦΙΪ ΫΘΚ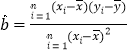 Θ§
Θ§![]() Θ©
Θ©
Θ®IIΘ©“―÷ΣΟΩΝΨΗΟ–ΆΚ≈Τϊ≥ΒΒΡ ’ΙΚΦέΗώΈΣ![]() Άρ‘ΣΘ§ΗυΨίΘ®IΘ©÷–Υυ«σΒΡΜΊΙιΖΫ≥ΧΘ§‘Λ≤β
Άρ‘ΣΘ§ΗυΨίΘ®IΘ©÷–Υυ«σΒΡΜΊΙιΖΫ≥ΧΘ§‘Λ≤β![]() ΈΣΚΈ÷Β ±Θ§œζ έ“ΜΝΨΗΟ–ΆΚ≈Τϊ≥ΒΥυΜώΒΟΒΡάϊ»σ
ΈΣΚΈ÷Β ±Θ§œζ έ“ΜΝΨΗΟ–ΆΚ≈Τϊ≥ΒΥυΜώΒΟΒΡάϊ»σ![]() Ήν¥σΘΩΘ®άϊ»σ=œζ έΦέΗώ- ’ΙΚΦέΗώΘ©
Ήν¥σΘΩΘ®άϊ»σ=œζ έΦέΗώ- ’ΙΚΦέΗώΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com