
【题目】用“算筹”表示数是我国古代计数方法之一,计数形式有纵式和横式两种,如图1所示.金元时期的数学家李冶在《测圆海镜》中记载:用“天元术”列方程,就是用算筹来表示方程中各项的系数.所谓“天元术”,即是一种用数学符号列方程的方法,“立天元一为某某”,意即“设![]() 为某某”.如图2所示的天元式表示方程
为某某”.如图2所示的天元式表示方程![]() ,其中
,其中![]() ,
,![]() ,…,
,…,![]() ,
,![]() 表示方程各项的系数,均为筹算数码,在常数项旁边记一“太”字或在一次项旁边记一“元”字,“太”或“元”向上每层减少一次幂,向下每层增加一次幂.
表示方程各项的系数,均为筹算数码,在常数项旁边记一“太”字或在一次项旁边记一“元”字,“太”或“元”向上每层减少一次幂,向下每层增加一次幂.

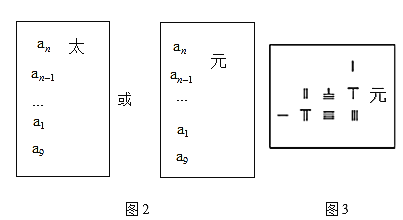
试根据上述数学史料,判断图3天元式表示的方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】如图1,四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点,满足
上一点,满足![]() ,
,![]() 为
为![]() 的中点,现将梯形沿
的中点,现将梯形沿![]() 折叠(如图2),使平面
折叠(如图2),使平面![]() 平面
平面![]() .
.
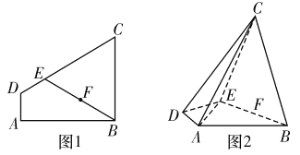
(1)求证:平面![]() 平面
平面![]() ;
;
(2)能否在线段![]() 上找到一点
上找到一点![]() (端点除外)使得直线
(端点除外)使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ?若存在,试确定点
?若存在,试确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线
为直线![]() 的倾斜角),以坐标原点
的倾斜角),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 时直线
时直线![]() 的普通方程;
的普通方程;
(2)直线![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
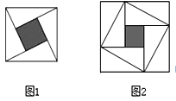
【题目】赵爽弦图(图1)是取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.图2是由弦图变化得到,它是由八个全等的直角三角形和中间的一个小正方形拼接而成.现随机向图2中大正方形的内部投掷一枚飞镖,若直角三角形的直角边长分别为2和3,则飞镖投中小正方形(阴影)区域的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() ,F为焦点,
,F为焦点,![]() 面积为1.
面积为1.
(1)求抛物线C的方程;
(2)过点P引圆![]() 的两条切线PA、PB,切线PA、PB与抛物线C的另一个交点分别为A、B,求直线AB斜率的取值范围.
的两条切线PA、PB,切线PA、PB与抛物线C的另一个交点分别为A、B,求直线AB斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
:![]() 的右焦点为
的右焦点为![]() ,半焦距
,半焦距![]() ,点
,点![]() 到右准线
到右准线![]() 的距离为
的距离为![]() ,过点
,过点![]() 作双曲线
作双曲线![]() 的两条互相垂直的弦
的两条互相垂直的弦![]() ,
,![]() ,设
,设![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() .
.
(1)求双曲线![]() 的标准方程;
的标准方程;
(2)证明:直线![]() 必过定点,并求出此定点坐标.
必过定点,并求出此定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)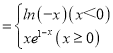 ,若关于x的方程f2(x)﹣af(x)+a﹣a2=0有四个不等的实数根,则a的取值范围是( )
,若关于x的方程f2(x)﹣af(x)+a﹣a2=0有四个不等的实数根,则a的取值范围是( )
A.![]() B.(﹣∞,﹣1)∪[1,+∞)
B.(﹣∞,﹣1)∪[1,+∞)
C.(﹣∞,﹣1)∪{1}D.(﹣1,0)∪{1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是定义在R上的两个周期函数,
是定义在R上的两个周期函数,![]() 的周期为4,
的周期为4,![]() 的周期为2,且
的周期为2,且![]() 是奇函数.当
是奇函数.当![]() 时,
时,![]() ,
,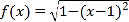 ,其中k>0.若在区间(0,9]上,关于x的方程
,其中k>0.若在区间(0,9]上,关于x的方程![]() 有8个不同的实数根,则k的取值范围是_____.
有8个不同的实数根,则k的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 、
、![]() 、
、![]() 都有
都有![]() ,满足
,满足![]() 的实数
的实数![]() 有且只有3个,给出下述四个结论:①满足题目条件的实数
有且只有3个,给出下述四个结论:①满足题目条件的实数![]() 有且只有2个:②满足题目条件的实数
有且只有2个:②满足题目条件的实数![]() 有且只有2个;③
有且只有2个;③![]() 在
在![]() 上单调递增;④
上单调递增;④![]() 的取值范围是
的取值范围是![]() .其中所有正确的个数是( )
.其中所有正确的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com