
如图,设椭圆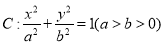 的左右焦点为
的左右焦点为 ,上顶点为
,上顶点为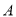 ,点
,点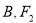 关于
关于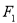 对称,且
对称,且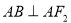
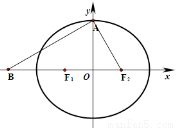
(1)求椭圆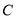 的离心率;
的离心率;
(2)已知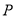 是过
是过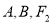 三点的圆上的点,若
三点的圆上的点,若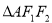 的面积为
的面积为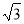 ,求点
,求点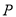 到直线
到直线 距离的最大值.
距离的最大值.
(1)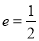 ;(2)4
;(2)4
【解析】
试题分析:(1)设椭圆的方程,用待定系数法求出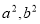 的值;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式
的值;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式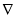 :计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论;(3)判断直线与圆的位置关系时,若两方程已知或圆心到直线的距离易表达,用几何法;若方程中含参数,或圆心到直线的距离的表达较繁琐,则用代数法.
:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论;(3)判断直线与圆的位置关系时,若两方程已知或圆心到直线的距离易表达,用几何法;若方程中含参数,或圆心到直线的距离的表达较繁琐,则用代数法.
试题解析:【解析】
(1)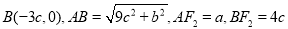 2分
2分
由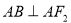 及勾股定理可知
及勾股定理可知 ,即
,即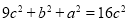 4分
4分
因为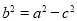 ,所以
,所以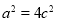 ,解得
,解得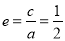 6分
6分
(2)由(1)可知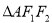 是边长为
是边长为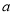 的正三角形,所以
的正三角形,所以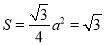
解得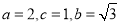 8分
8分
由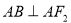 可知直角三角形
可知直角三角形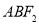 的外接圆以
的外接圆以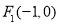 为圆心,半径
为圆心,半径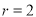
即点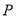 在圆
在圆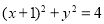 上, 10分
上, 10分
因为圆心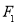 到直线
到直线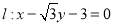 的距离为
的距离为 12分
12分
故该圆与直线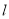 相切,所以点
相切,所以点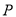 到直线
到直线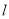 的最大距离为
的最大距离为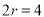 13分
13分
考点:1、椭圆的离心率;2、直线与圆的应用.


科目:高中数学 来源:2015届福建省高三10月月考理科数学试卷(解析版) 题型:解答题
(本小题满分7分)选修4-5:不等式选讲
已知不等式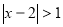 的解集与关于
的解集与关于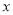 的不等式
的不等式 的解集相等.
的解集相等.
(Ⅰ)求实数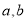 的值.
的值.
(Ⅱ)求函数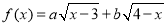 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2015届福建省、德化一中高三9月摸底考试文科数学试卷(解析版) 题型:选择题
设 与
与 是定义在同一区间
是定义在同一区间 上的两个函数,若对任意的
上的两个函数,若对任意的 ,都有
,都有 ,则称
,则称 和
和 在
在 上是“密切函数”,
上是“密切函数”, 称为“密切区间”,设
称为“密切区间”,设 与
与 在
在 上是“密切函数”,则它的“密切区间”可以是( )
上是“密切函数”,则它的“密切区间”可以是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届福建省八县(市高三上学期半期联考文科数学试卷(解析版) 题型:填空题
如图,点(x,y)在四边形ABCD内部和边界上运动,那么3x-y的最小值为________.
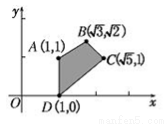
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com