
分析 (1)根据g(x)的单调性,得到关于a,b的方程组,求出a,b的值即可;
(2)令t=|lgx-1|,则t∈(0,1],问题转化为$t+\frac{2+2k}{t}-3k-3≥0$对任意t∈(0,1]恒成立,令$h(t)=t+\frac{2+2k}{t}-3k-3$,t∈(0,1],通过讨论k的范围,结合函数的单调性,确定k的具体范围即可.
解答 解:(1)g(x)=a(x-1)2+b-a,因为a>0,所以g(x)在区间[1,3]上是增函数,
故$\left\{{\begin{array}{l}{g(1)=1}\\{g(3)=5}\end{array}}\right.$,解得$\left\{{\begin{array}{l}{a=1}\\{b=2}\end{array}}\right.$.
(2)由已知可得$f(x)=x+\frac{2}{x}-2$,$f(|lgx-1|)+k•\frac{2}{|lgx-1|}-3k≥1$,
即$|lgx-1|+\frac{2}{|lgx-1|}-2+\frac{2k}{|lgx-1|}-3k≥1$,
令t=|lgx-1|,则t∈(0,1],$t+\frac{2+2k}{t}-3k-3≥0$对任意t∈(0,1]恒成立,
令$h(t)=t+\frac{2+2k}{t}-3k-3$,t∈(0,1],则:
①当k=-1时,h(t)=t≥0成立;
②当k<-1时,$h(t)=t+\frac{2+2k}{t}-3k-3$在(0,1]上为增函数,t→0+时,h(t)→-∞,舍去;
③当k>-1时,h(t)在$(0,\sqrt{2+2k}]$上为减函数,在$[\sqrt{2+2k},+∞)$上为增函数,
若$\sqrt{2+2k}<1$,即$-1<k<-\frac{1}{2}$时,$h{(t)_{min}}=h(\sqrt{2+2k})=2\sqrt{2+2k}-3k-3≥0$,
得$-1≤k≤-\frac{1}{9}$,∴$-1<k<-\frac{1}{2}$.
若$\sqrt{2+2k}≥1$,即$k≥-\frac{1}{2}$时,h(t)在(0,1]上为减函数,h(t)min=h(1)=-k≥0,
∴$-\frac{1}{2}≤k≤0$,
综上,k的取值范围为[-1,0].
点评 本题考查了二次函数的性质,考查函数的单调性、求函数的最值问题,考查换元思想、分类讨论思想,是一道综合题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
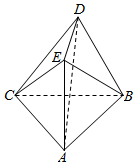 如图,空间几何体ABCDE中,平面ABC⊥平面BCD,AE⊥平面ABC.
如图,空间几何体ABCDE中,平面ABC⊥平面BCD,AE⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{13}{e^3},\frac{7}{e^2}]$ | B. | $(\frac{13}{e^3},\frac{7}{e^2}]$ | C. | $[\frac{7}{e^2},\frac{3}{e}]$ | D. | $(\frac{7}{e^2},\frac{3}{e}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com