
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也必要条件 |
分析 由cosA=$\frac{b}{c}$,利用余弦定理可得:b2+a2=c2,C=90°,△ABC为Rt△.反之不成立,例如A为直角,则cosA=0.
解答 解:cosA=$\frac{b}{c}$⇒$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{b}{c}$,化为:b2+a2=c2⇒C=90°,⇒△ABC为Rt△.
反之不成立,例如A为直角,则cosA=0≠$\frac{b}{c}$.
∴“cosA=$\frac{b}{c}$”是“△ABC为Rt△”的充分不必要条件.
故选:A.
点评 本题考查了余弦定理、勾股定理的逆定理、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
| 年龄段分组 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 频数 | 300 | 320 | 160 | 160 | 40 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
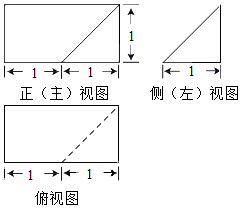
| A. | $\frac{1}{2}$ | B. | $\frac{5}{6}$ | C. | 1 | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
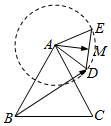 如图,等边△ABC的边长为2,△ADE也是等边三角形且边长为1,M为DE的中心,在△ABC所在平面内,△ADE绕A逆时针旋转一周,$\overrightarrow{BD}$•$\overrightarrow{AM}$的最大值为( )
如图,等边△ABC的边长为2,△ADE也是等边三角形且边长为1,M为DE的中心,在△ABC所在平面内,△ADE绕A逆时针旋转一周,$\overrightarrow{BD}$•$\overrightarrow{AM}$的最大值为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{4}$+$\sqrt{3}$ | C. | $\frac{3+\sqrt{3}}{4}$ | D. | $\frac{3}{4}$+2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{12}$个单位 | B. | 向右平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{12}$个单位 | D. | 向左平移$\frac{π}{4}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a|0≤a<1} | B. | {a|-1<a≤0} | C. | {a|-1<a<1} | D. | {a|a∈R,a∉Z} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com