
分析 (I)根据绝对值不等式的性质化简消去x,再利用基本不等式得出结论;
(II)讨论a的范围,去绝对值符号解出a的范围.
解答 (I)证明:f(x)=|$\frac{x}{2}$+$\frac{1}{2a}$|+|$\frac{x}{2}$-$\frac{a}{2}$|≥|($\frac{x}{2}+\frac{1}{2a}$)-($\frac{x}{2}-\frac{a}{2}$)|=|$\frac{a}{2}+\frac{1}{2a}$|=$\frac{a}{2}+\frac{1}{2a}$≥2$\sqrt{\frac{a}{2}×\frac{1}{2a}}$=1.
∴f(x)≥1.
(II)解:∵f(x)<5,即|3+$\frac{1}{2a}$|+|3-$\frac{a}{2}$|<5,
∴$\frac{1}{2a}$+|3-$\frac{a}{2}$|-2<0,
当0<a<6时,$\frac{1}{2a}$+3-$\frac{a}{2}$-2<0,解得1+$\sqrt{2}$<a<6,
当a≥6时,$\frac{1}{2a}$+$\frac{a}{2}-3$-2<0,解得6≤a<5+2$\sqrt{6}$,
综上,a的取值范围是(1+$\sqrt{2}$,5+2$\sqrt{6}$).
点评 本题考查了绝对值不等式的性质与解法,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | $\sqrt{21}$ | C. | $\frac{\sqrt{45}}{2}$ | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
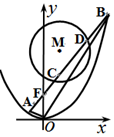 已知抛物线G的顶点在原点,焦点在y轴正半轴上,抛物线上的点P(m,4)到其焦点F的距离等于5.
已知抛物线G的顶点在原点,焦点在y轴正半轴上,抛物线上的点P(m,4)到其焦点F的距离等于5.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
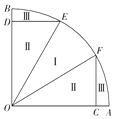 现有一个以OA、OB为半径的扇形池塘,在OA、OB上分别取点C、D,作DE∥OA、CF∥OB分别交弧AB于点E、F,且BD=AC,现用渔网沿着DE、EO、OF、FC将池塘分成如图所示的养殖区域.已知OA=1km,∠AOB=$\frac{π}{2}$,∠EOF=θ(0<θ<$\frac{π}{2}$).
现有一个以OA、OB为半径的扇形池塘,在OA、OB上分别取点C、D,作DE∥OA、CF∥OB分别交弧AB于点E、F,且BD=AC,现用渔网沿着DE、EO、OF、FC将池塘分成如图所示的养殖区域.已知OA=1km,∠AOB=$\frac{π}{2}$,∠EOF=θ(0<θ<$\frac{π}{2}$).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com