
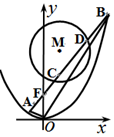
 已知抛物线G的顶点在原点,焦点在y轴正半轴上,抛物线上的点P(m,4)到其焦点F的距离等于5.
已知抛物线G的顶点在原点,焦点在y轴正半轴上,抛物线上的点P(m,4)到其焦点F的距离等于5.分析 (Ⅰ)利用点P(m,4)到抛物线的准线距离为5,结合准线方程为y+1=0,求解p,即可求解抛物线G的方程.
(Ⅱ)显然直线l的斜率存在,设其斜率为k,由于l过焦点F(0,1),直线l的方程为y=kx+1,取CD的中点N,连接MN,什么N点也是线段AB的中点,设A(x1,y1)、B(x2,y2)、N(x0,y0),联立$\left\{\begin{array}{l}{x^2}=4y\\ y=kx+1\end{array}\right.$利用韦达定理转化推出$\frac{{(2{k^2}+1)-4}}{2k-1}=-\frac{1}{k}$,求出k,然后求解三角形的面积.
解答 解:(Ⅰ)由题知,点P(m,4)到抛物线的准线距离为5,所以准线方程为y+1=0,$\frac{p}{2}=1$,
抛物线G的方程为x2=4y…(4分)
(Ⅱ)显然直线l的斜率存在,设其斜率为k,由于l过焦点F(0,1),
所以直线l的方程为y=kx+1…(5分)
取CD的中点N,连接MN,则MN⊥CD,由于|AC|=|BD|,所以N点也是线段AB的中点,
设A(x1,y1)、B(x2,y2)、N(x0,y0),则${x_0}=\frac{{{x_1}+{x_2}}}{2}$,${y_0}=\frac{{{y_1}+{y_2}}}{2}$
由$\left\{\begin{array}{l}{x^2}=4y\\ y=kx+1\end{array}\right.$得x2-4kx-4=0,所以x1+x2=4k,∴x0=2k,${y_0}=2{k^2}+1$,即N(2k,2k2+1)…(9分)
∵${k_{MN}}=-\frac{1}{k}$,即$\frac{{(2{k^2}+1)-4}}{2k-1}=-\frac{1}{k}$,
整理得2k3-k-1=0,即(k-1)(2k2+2k+1)=0,∴k=1,
∵|AB|=y1+y2+2=(x1+1)+(x2+1)+2=8
原点到直线AB的距离为$d=\frac{1}{{\sqrt{2}}}=\frac{{\sqrt{2}}}{2}$…(11分)
∴${S_{△OAB}}=\frac{1}{2}|AB|×d=2\sqrt{2}$…(12分)
点评 本题考查抛物线的简单性质以及抛物线方程的求法,考查转化思想以及计算能力.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{5}-1}}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{7}$ | B. | $-\frac{7}{5}$ | C. | $\frac{10}{7}$ | D. | $-\frac{10}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,e2) | B. | (e-2,+∞) | C. | (e2,+∞) | D. | (e-2,e2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{7}{6}$ | D. | $\frac{{\sqrt{42}}}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com