
分析 (Ⅰ)推导出${f}^{'}(x)=\frac{1}{x}-ax+(1-a)=\frac{-a{x}^{2}+(1-a)x+1}{x}$,由a的取值进行分类,结合导数的性质能求出函数f(x)的单调区间.
(Ⅱ)当a=-2时,$g(x)=lnx+{x^2}+x-\frac{11}{2}$,x>0.推导出(x1+x2)2+(x1+x2)-11=x1x2-ln(x1x2),令t=x1x2,则由ϕ(t)=t-lnt得:$ϕ'(t)=1-\frac{1}{t}=\frac{t-1}{t}$,由此利用导数性质能求出x1+x2的最小值.
解答 (本小题满分12分)
解:(Ⅰ)∵f(x)=lnx-$\frac{1}{2}$ax2+(1-a)x+1,a∈R,
∴${f}^{'}(x)=\frac{1}{x}-ax+(1-a)=\frac{-a{x}^{2}+(1-a)x+1}{x}$,…(1分)
当a≤0时,∵x>0,∴f′(x)>0.∴f(x)在(0,+∞)上是递增函数,
即f(x)的单调递增区间为(0,+∞),无递减区间.…(3分)
当a>0时,${f}^{'}(x)=\frac{-a{x}^{2}+(1-a)x+1}{x}$=-$\frac{a(x-\frac{1}{a})(x+1)}{x}$,
令f′(x)=0,得$x=\frac{1}{a}$.∴当$x∈(0,\frac{1}{a})$时,f′(x)>0;
当$x∈(\frac{1}{a},+∞)$时,f′(x)<0.
∴f(x)在$(0,\frac{1}{a})$上是增函数,在($\frac{1}{a},+∞$)上是减函数.
∴f(x)的单调递增区间为(0,$\frac{1}{a}$),单调递减区间为($\frac{1}{a},+∞$).…(5分)
综上,当a≤0时,f(x)的单调递增区间为(0,+∞),无递减区间;
当a>0时,f(x)的单调递增区间为(0,$\frac{1}{a}$),单调递减区间为($\frac{1}{a}$,+∞).…(6分)
(Ⅱ)当a=-2时,$g(x)=lnx+{x^2}+x-\frac{11}{2}$,x>0.
由g(x1)+g(x2)+x1x2=0,即$ln{x_1}+x_1^2+{x_1}+ln{x_2}+x_2^2+{x_2}+{x_1}{x_2}-11=0$,
从而(x1+x2)2+(x1+x2)-11=x1x2-ln(x1x2),…(8分)
令t=x1x2,则由ϕ(t)=t-lnt得:$ϕ'(t)=1-\frac{1}{t}=\frac{t-1}{t}$,
可知,ϕ(t)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增.
∴ϕ(t)≥ϕ(1)=1,…(10分)
∴(x1+x2)2+(x1+x2)-11≥1,∴(x1+x2+4)(x1+x2-3)≥0
又∵x1>0,x2>0,∴x1+x2≥3.
当且仅当x1,2=$\frac{3±\sqrt{5}}{2}$时取等号. …(11分)
则x1+x2的最小值是3.…(12分)
点评 本题考查函数的单调区间的求法,考查两数和的最小值的求法,考查导数性质、构造法、函数单调性等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、分类与整合思想,是中档题.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
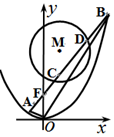 已知抛物线G的顶点在原点,焦点在y轴正半轴上,抛物线上的点P(m,4)到其焦点F的距离等于5.
已知抛物线G的顶点在原点,焦点在y轴正半轴上,抛物线上的点P(m,4)到其焦点F的距离等于5.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{e}})$ | B. | $[{\frac{1}{4},\frac{1}{e}})$ | C. | $({0,\frac{1}{4}}]$ | D. | $({\frac{1}{4},e})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | -14 | C. | 14 | D. | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com