
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{5}-1}}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 由向量数量积的坐标运算及点差法作差求得$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{{b}^{2}}{{a}^{2}}$×$\frac{{x}_{1}+{x}_{2}}{{y}_{1}+{y}_{2}}$,代入即可求得a和b的关系,即可求得椭圆的离心率.
解答 解:设A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4),
由$\overrightarrow{AM}$=λ$\overrightarrow{MC}$,即(2-x1,1-y1)=λ(x3-2,y3-1),
则$\left\{\begin{array}{l}{{x}_{1}+λ{x}_{3}=2+2λ}\\{{y}_{1}+λ{y}_{3}=1+λ}\end{array}\right.$,同理可得:$\left\{\begin{array}{l}{{x}_{2}+λ{x}_{4}=2+2λ}\\{{y}_{2}+λ{y}_{4}=1+λ}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}+λ({x}_{3}+{x}_{4})=4(1+λ)}\\{{y}_{1}+{y}_{2}+λ({y}_{3}+{y}_{4})=2(1+λ)}\end{array}\right.$,则2[(y1+y2)+λ(y3+y4)]=1[(x1+x2)+λ(x3+x4)],
将点A,B的坐标代入椭圆方程作差可得:$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{{b}^{2}}{{a}^{2}}$×$\frac{{x}_{1}+{x}_{2}}{{y}_{1}+{y}_{2}}$,
即-$\frac{1}{2}$=-$\frac{{b}^{2}}{{a}^{2}}$×$\frac{{x}_{1}+{x}_{2}}{{y}_{1}+{y}_{2}}$,则a2(y1+y2)=2b2(x1+x2)①,
同理可得:a2(y3+y4)=2b2(x3+x4)②,
①+②得:a2[(y1+y2)+(y3+y4)]=2b2[(x1+x2)+(x3+x4)],
∴2[(y1+y2)+λ(y3+y4)]=1[(x1+x2)+λ(x3+x4)],
∴$\frac{{a}^{2}}{2}$=$\frac{2{b}^{2}}{1}$
则$\frac{{b}^{2}}{{a}^{2}}$=$\frac{1}{4}$,
则椭圆的离心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{3}}{2}$,
故选D.
点评 本题考查椭圆的离心率的求法.考查向量坐标运算,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
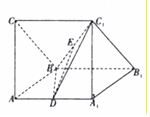 在如图所示的直三棱柱ABC-A1B1C1中,面AA1B1B和面AA1C1C都是边长为1的正方形且互相垂直,D为AA1的中点,E为BC1的中点.
在如图所示的直三棱柱ABC-A1B1C1中,面AA1B1B和面AA1C1C都是边长为1的正方形且互相垂直,D为AA1的中点,E为BC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {0} | C. | (-1,1) | D. | (-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2017}$ | B. | $\frac{2π}{2017}$ | C. | $\frac{4π}{2017}$ | D. | $\frac{π}{4034}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
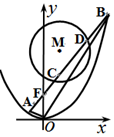 已知抛物线G的顶点在原点,焦点在y轴正半轴上,抛物线上的点P(m,4)到其焦点F的距离等于5.
已知抛物线G的顶点在原点,焦点在y轴正半轴上,抛物线上的点P(m,4)到其焦点F的距离等于5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com