
| A. | $(\frac{a}{4},0)$ x=-$\frac{a}{4}$ | B. | $(0,\frac{a}{4})$ y=-$\frac{a}{4}$ | C. | $(\frac{1}{4a},0)$ x=-$\frac{1}{4a}$ | D. | $(0,\frac{1}{4a})$ y=-$\frac{1}{4a}$ |
分析 由条件利用抛物线的标准方程,以及简单性质,分类讨论求出它的焦点坐标和准线方程.
解答 解:当a>0时,抛物线y=ax2(a≠0),
即为x2=$\frac{y}{a}$,
开口向上,2p=$\frac{1}{a}$,$\frac{p}{2}$=$\frac{1}{4a}$,
焦点坐标为(0,$\frac{1}{4a}$),准线方程为y=-$\frac{1}{4a}$.
当a<0时,抛物线y=ax2(a≠0),
即为x2=$\frac{y}{a}$,
开口向下,2p=$\frac{1}{a}$,$\frac{p}{2}$=$\frac{1}{4a}$,
焦点坐标为(0,$\frac{1}{4a}$),准线方程为y=-$\frac{1}{4a}$.
综上可得,抛物线的焦点坐标为(0,$\frac{1}{4a}$),准线方程为y=-$\frac{1}{4a}$.
故选:D.
点评 本题主要考查抛物线的标准方程,以及简单性质的应用,体现了分类讨论的数学思想,属于基础题.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\sqrt{3}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
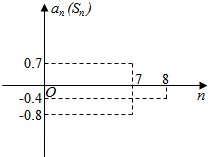 已知等差数列{an}的前n项和为Sn,在同一坐标系中,an=f(n)及Sn=g(n)的部分图象如图所示.
已知等差数列{an}的前n项和为Sn,在同一坐标系中,an=f(n)及Sn=g(n)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com