
分析 (I)利用等差数列的通项公式及其对数的运算性质即可得出.
(II)bn=$\frac{{na_n^{\;}}}{{(2n+1)•{2^n}}}$=$\frac{n}{2n+1}$,由b1,bm,bn成等比数列,可得$(\frac{m}{2m+1})^{2}$=$\frac{1}{3}×\frac{n}{2n+1}$,即$\frac{3}{n}$=$\frac{-2{m}^{2}+4m+1}{{m}^{2}}$,由-2m2+4m+1>0,解出即可得出.
(Ⅲ)${c_n}=\frac{2n+4}{{n(n+1){2^n}}}=4[{\frac{1}{{n•{2^n}}}-\frac{1}{{(n+1)•{2^{n+1}}}}}]$,利用“裂项求和”方法与数列的单调性即可得出.
解答 解:(Ⅰ)∵对任意的n∈N*,n≥2,$log_2^{\;}{a_n}=1+log_2^{\;}{a_{n-1}}$,即:$log_2^{\;}{a_n}-log_2^{\;}{a_{n-1}}=1$,
∴数列{$log_2^{\;}{a_n}$}是首相为$log_2^{\;}{a_1}=log_2^{\;}2=1$,公差为1的等差数列.
∴$log_2^{\;}{a_n}=1+1×(n-1)=n$,
∴${a}_{n}={2}^{n}$.
(Ⅱ)bn=$\frac{{na_n^{\;}}}{{(2n+1)•{2^n}}}$=$\frac{n}{2n+1}$,
若b1,bm,bn成等比数列,
则$(\frac{m}{2m+1})^{2}$=$\frac{1}{3}×\frac{n}{2n+1}$,即$\frac{{m}^{2}}{4{m}^{2}+4m+1}$=$\frac{n}{6n+3}$.
可得$\frac{3}{n}$=$\frac{-2{m}^{2}+4m+1}{{m}^{2}}$,
∴-2m2+4m+1>0,解得:$1-\frac{\sqrt{6}}{2}$<m<1+$\frac{\sqrt{6}}{2}$.
又m∈N*,且m>1,∴m=2,此时n=12.
故当且仅当m=2,n=12.
使得b1,bm,bn成等比数列.
(Ⅲ)证明:${c_n}=\frac{2n+4}{{n(n+1){2^n}}}=4[{\frac{1}{{n•{2^n}}}-\frac{1}{{(n+1)•{2^{n+1}}}}}]$,
∴Sn=c1+c2+c3+…+cn=$4[{\frac{1}{{1×{2^1}}}-\frac{1}{{2×{2^2}}}+\frac{1}{{2×{2^2}}}-\frac{1}{{3×{2^3}}}+…+\frac{1}{{({n-1})×{2^{n-1}}}}-\frac{1}{{n×{2^n}}}+\frac{1}{{n×{2^n}}}-\frac{1}{{({n+1})×{2^{n+1}}}}}]$
$\begin{array}{l}=4[{\frac{1}{{1×{2^1}}}-\frac{1}{{({n+1})×{2^{n+1}}}}}]\\=2-\frac{1}{{({n+1})×{2^{n-1}}}}\end{array}$
∴${S_n}<2,且{S_n}≥{S_1}=\frac{3}{2}$,即结论$\frac{3}{2}≤{S_n}<2$成立.
点评 本题考查了递推关系、等差数列与等比数列的通项公式与前n项和公式、“裂项求和”方法、对数的运算性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
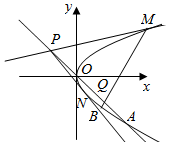 已知抛物线C:y2=2px(p>0)的交点为F,过F且倾斜角为$\frac{π}{4}$的直线l被抛物线C截得的线段长为8.
已知抛物线C:y2=2px(p>0)的交点为F,过F且倾斜角为$\frac{π}{4}$的直线l被抛物线C截得的线段长为8.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 100 | B. | 99$\frac{1}{2}$ | C. | 99 | D. | 98$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{{\sqrt{6}}}{9}$ | B. | $\frac{{\sqrt{6}}}{9}$ | C. | -$\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 54 | B. | 36 | C. | 24 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| X | 110 | 120 | 125 | 130 | 135.2 |
| P | 0.1 | 0.2 | 0.4 | 0.1 | 0.2 |
| Y | 100 | 115 | 125 | 130 | 145 |
| P | 0.1 | 0.2 | 0.4 | 0.1 | 0.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com