
���� ��1��������ѧ���ɷ�֤����������֤n=2�����������n=k�����۳��������ɺ���y=ax+$\frac{b}{x}$�����ʣ���֤n=k+1Ҳ������
��2��������ѧ���ɷ�֤����������֤n=2�����������n=k�����۳������ٽ���������������������ɵõ�n=k+1Ҳ������������֤��
��� ֤������1����n=2ʱ��a2=$\frac{1}{2}$+1=$\frac{3}{2}$��$\sqrt{2}$��������
����n=kʱ��ak��$\sqrt{2}$������
��n=k+1ʱ��ak+1=$\frac{1}{2}$ak+$\frac{1}{{a}_{k}}$��$\frac{1}{2}$•$\sqrt{2}$+$\frac{1}{\sqrt{2}}$=$\sqrt{2}$��
��n=k+1ʱ��Ҳ������
��һ��n��N*��n��2��an��$\sqrt{2}$��
��2����n=2ʱ��b2=$\frac{2}{\sqrt{{{a}_{2}}^{2}-2}}$=$\frac{2}{\sqrt{\frac{9}{4}-2}}$=4��
c2=$\frac{4{a}_{2}}{{{a}_{2}}^{2}-2}$=$\frac{4��\frac{3}{2}}{\frac{9}{4}-2}$=24��b2��c2������������
����n=k��bk��ck������������
����n=k+1ʱ��bk+1=$\frac{2}{\sqrt{{{a}_{k+1}}^{2}-2}}$=$\frac{2}{\sqrt{��\frac{1}{2}{a}_{k}+\frac{1}{{a}_{k}}��^{2}-2}}$=$\frac{2}{\frac{1}{2}{a}_{k}-\frac{1}{{a}_{k}}}$
=$\frac{4{a}_{k}}{{{a}_{k}}^{2}-2}$=ck��������
ck+1=$\frac{4{a}_{k+1}}{{{a}_{k+1}}^{2}-2}$=$\frac{8{a}_{k}��{{a}_{k}}^{2}+2��}{��{{a}_{k}}^{2}-2��^{2}}$=$\frac{4{a}_{k}}{{{a}_{k}}^{2}-2}$•$\frac{2��{{a}_{k}}^{2}+2��}{{{a}_{k}}^{2}-2}$
=ck•2��1+$\frac{4}{{{a}_{k}}^{2}-2}$��=ck•2��1+bk2������Ϊ��������
���ж�һ��n��N*��n��2��bn��cn������������
���� ���⿼����ѧ���ɷ������ã�ͬʱ���鲻��ʽ�����ʺͻ������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
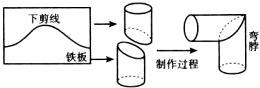 ����ʦ���ڴ�����Ͳ�䲱ʱ��Ϊȷ���Խӳ�ֱ�ǣ��������ϵ��¼�����������������$y=acos\frac{x}{a}$��һ�����ڵ�ͼ����ͼ�����䲱��ֱ��Ϊ12cmʱ��aӦ��6cm��
����ʦ���ڴ�����Ͳ�䲱ʱ��Ϊȷ���Խӳ�ֱ�ǣ��������ϵ��¼�����������������$y=acos\frac{x}{a}$��һ�����ڵ�ͼ����ͼ�����䲱��ֱ��Ϊ12cmʱ��aӦ��6cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
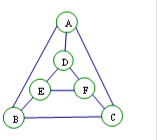 ִ��ij�������Ի�����ذ�����Ҫ���ͼ������СԲͿɫ��
ִ��ij�������Ի�����ذ�����Ҫ���ͼ������СԲͿɫ��| A�� | $\frac{9}{16}$ | B�� | $\frac{3}{8}$ | C�� | $\frac{18}{25}$ | D�� | $\frac{12}{25}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �۽������� | B�� | ��������� | C�� | ֱ�������� | D�� | ��״����ȷ�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com