
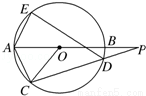
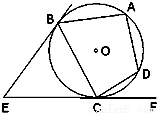
(2014•江苏模拟)如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,AE=AC,求证:∠PDE=∠POC.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.2二阶矩阵与平面向量的乘法(解析版) 题型:填空题
(2014•上海模拟)已知正数a,b满足a+b=2,则行列式 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:选择题
(2006•朝阳区二模)将直线x+ y=0绕原点按顺时针方向旋转30°,所得直线与圆(x﹣2)2+y2=3的位置关系是( )
y=0绕原点按顺时针方向旋转30°,所得直线与圆(x﹣2)2+y2=3的位置关系是( )
A.直线与圆相离 B.直线与圆相交但不过圆心
C.直线与圆相切 D.直线过圆心
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.2平面与圆柱面的截线练习卷(解析版) 题型:选择题
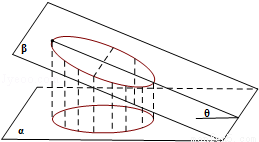
(2014•安徽模拟)如图,一个底面半径为R的圆柱被与其底面所成角为θ(00<θ<900)的平面所截,截面是一个椭圆.当θ为30°时,这个椭圆的离心率为( )
A. B.
B.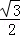 C.
C.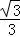 D.
D.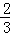
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷(解析版) 题型:填空题
(2014•陕西模拟)如图,EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=46°,∠DCF=32°,则∠A的大小为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷(解析版) 题型:选择题
如图PA是圆O的切线,切点为A,PA=2,AC是圆O的直径,PC与圆O交于点B,PB=1,则圆O的半径R=( )

A.2 B.3 C. D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷(解析版) 题型:填空题
(2010•湖南模拟)如图,AB为半圆O的直径,OC⊥AB,OD平分∠BOC,交半圆于点D,AD交OC于点E,则∠AEO的度数是 度.
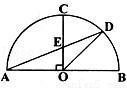
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修1-2 3.2数学证明练习卷(解析版) 题型:选择题
(2014•陕西模拟)已知[x]表示不超过实数x的最大整数(x∈R),如:[﹣1.3]=﹣2,[0.8]=0,[3.4]=3.定义{x}=x﹣[x],求{ }+{
}+{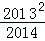 }+{
}+{ }+…+{
}+…+{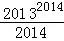 }=( )
}=( )
A.1006 B.1007 C.1008 D.2014
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com