
【题目】已知函数![]() .
.
![]() Ⅰ
Ⅰ![]() 若曲线
若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数
垂直,求函数![]() 的单调区间;
的单调区间;
![]() Ⅱ
Ⅱ![]() 若对于
若对于![]() 都有
都有![]() 成立,试求a的取值范围;
成立,试求a的取值范围;
![]() Ⅲ
Ⅲ![]() 记
记![]() 当
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上有两个零点,求实数b的取值范围.
上有两个零点,求实数b的取值范围.
【答案】解: (I) 直线![]() 的斜率为1.
的斜率为1.
函数![]() 的定义域为
的定义域为![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
所以![]() .
.![]() .
.
由![]() 解得
解得![]() ;由
;由![]() 解得
解得![]() .
.
所以![]() 的单调增区间是
的单调增区间是![]() ,单调减区间是
,单调减区间是![]() . ……………………4分
. ……………………4分
(II)![]() ,
,
由![]() 解得
解得![]() ;由
;由![]() 解得
解得![]() .
.
所以![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减.
上单调递减.
所以当![]() 时,函数
时,函数![]() 取得最小值,
取得最小值,![]() .
.
因为对于![]() 都有
都有![]() 成立,
成立,
所以![]() 即可.
即可.
则![]() . 由
. 由![]() 解得
解得![]() .
.
所以![]() 的取值范围是
的取值范围是![]() . ………………………………8分
. ………………………………8分
(III)依题得![]() ,则
,则![]() .
.
由![]() 解得
解得![]() ;由
;由![]() 解得
解得![]() .
.
所以函数![]() 在区间
在区间![]() 为减函数,在区间
为减函数,在区间![]() 为增函数.
为增函数.
又因为函数![]() 在区间
在区间![]() 上有两个零点,所以
上有两个零点,所以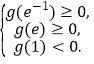
解得![]() .
.
所以![]() 的取值范围是
的取值范围是![]() . ……………………………………13分
. ……………………………………13分
【解析】
![]() Ⅰ
Ⅰ![]() 求出函数的定义域,在定义域内,求出导数大于0的区间,即为函数的增区间,求出导数小于0的区间即为函数的减区间;
求出函数的定义域,在定义域内,求出导数大于0的区间,即为函数的增区间,求出导数小于0的区间即为函数的减区间;![]() Ⅱ
Ⅱ![]() 根据函数的单调区间求出函数的最小值,要使
根据函数的单调区间求出函数的最小值,要使![]() 恒成立,需使函数的最小值大于
恒成立,需使函数的最小值大于![]() ,从而求得a的取值范围;
,从而求得a的取值范围;![]() Ⅲ
Ⅲ![]() 利用导数的符号求出单调区间,再根据函数
利用导数的符号求出单调区间,再根据函数![]() 在区间
在区间![]() 上有两个零点,得到
上有两个零点,得到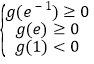 ,解出实数b的取值范围.
,解出实数b的取值范围.
![]() Ⅰ
Ⅰ![]() 直线
直线![]() 的斜率为1,函数
的斜率为1,函数![]() 的定义域为
的定义域为![]() ,
,
因为![]() ,所以,
,所以,![]() ,所以,
,所以,![]() .
.
所以,![]() ,
,![]() 由
由 ![]() 解得
解得![]() ;由
;由![]() 解得
解得![]() .
.
所以![]() 的单调增区间是
的单调增区间是![]() ,单调减区间是
,单调减区间是![]() .
.
![]() Ⅱ
Ⅱ![]()
![]() ,由
,由![]() ,解得
,解得![]() ;由
;由![]() 解得
解得![]() .
.
所以,![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减.
上单调递减.
所以,当![]() 时,函数
时,函数![]() 取得最小值,
取得最小值,![]() 因为对于
因为对于![]() 都有
都有![]() 成立,
成立,
所以,![]() 即可
即可![]() 则
则![]() 由
由![]() 解得
解得![]() .
.
所以,a的取值范围是![]() .
.
![]() Ⅲ
Ⅲ![]() 依题得
依题得![]() ,则
,则![]() .
.
由![]() 解得
解得![]() ; 由
; 由![]() 解得
解得![]() .
.
所以函数![]() 在区间
在区间![]() 为减函数,在区间
为减函数,在区间![]() 为增函数.
为增函数.
又因为函数![]() 在区间
在区间![]() 上有两个零点,所以
上有两个零点,所以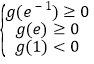 ,
,
解得![]() 所以,b的取值范围是
所以,b的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】设点A,B的坐标分别为(-2,0),(2,0)直线AM,BM相交于点M,且它们的斜率之积是-![]() .
.
(1)求点M的轨迹E的方程;
(2)设直线l:y=kx与E交于C,D两点,F1(-1,0),F2(1,0),若E上存在点P,使得![]() ,求实数k的取值范围.
,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店销售某海鲜,统计了春节前后50天该海鲜的需求量![]() (
(![]() ,单位:公斤),其频率分布直方图如图所示,该海鲜每天进货1次,商店每销售1公斤可获利50元;若供大于求,剩余的削价处理,每处理1公斤亏损10元;若供不应求,可从其它商店调拨,销售1公斤可获利30元.假设商店每天该海鲜的进货量为14公斤,商店的日利润为
,单位:公斤),其频率分布直方图如图所示,该海鲜每天进货1次,商店每销售1公斤可获利50元;若供大于求,剩余的削价处理,每处理1公斤亏损10元;若供不应求,可从其它商店调拨,销售1公斤可获利30元.假设商店每天该海鲜的进货量为14公斤,商店的日利润为![]() 元.
元.

(1)求商店日利润![]() 关于需求量
关于需求量![]() 的函数表达式;
的函数表达式;
(2)假设同组中的每个数据用该组区间的中点值代替.
①求这50天商店销售该海鲜日利润的平均数;
②估计日利润在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解全校高中学生五一小长假参加实践活动的情况,抽查了100名学生,统计他们假期参加实践活动的时间,绘成的频率分布直方图如图所示.
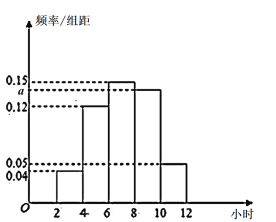
(1)估计这100名学生参加实践活动时间的众数、中位数和平均数.
(2)估计这100名学生参加实践活动时间的上四分位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() ,现以极点
,现以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的非负半轴建立平面直角坐标系,曲线
轴的非负半轴建立平面直角坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)若曲线![]() 为曲线
为曲线![]() 关于直线
关于直线![]() 的对称曲线,点
的对称曲线,点![]() 分别为曲线
分别为曲线![]() 、曲线
、曲线![]() 上的动点,点
上的动点,点![]() 坐标为
坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,摄影爱好者在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为![]() ,已知摄影爱好者的身高约为
,已知摄影爱好者的身高约为![]() 米(将眼睛S距地面的距离SA按
米(将眼睛S距地面的距离SA按![]() 米处理).
米处理).
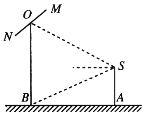
(1)求摄影爱好者到立柱的水平距离AB和立柱的高度OB;
(2)立柱的顶端有一长为2米的彩杆MN,且MN绕其中点O在摄影爱好者与立柱所在的平面内旋转.在彩杆转动的任意时刻,摄影爱好者观察彩杆MN的视角![]() (设为
(设为![]() )是否存在最大值?若存在,请求出
)是否存在最大值?若存在,请求出![]() 取最大值时
取最大值时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将![]() 这9个正整数分别写在三张卡片上,要求每一张卡片上的任意两数之差都不在这张卡片上,现在第一张卡片上已经写有
这9个正整数分别写在三张卡片上,要求每一张卡片上的任意两数之差都不在这张卡片上,现在第一张卡片上已经写有![]() 和
和![]() ,第二张卡片上写有
,第二张卡片上写有![]() ,第三张卡片上写有
,第三张卡片上写有![]() ,则
,则![]() 应该写在第__________张卡片上;第三张卡片上的所有书组成的集合是__________.
应该写在第__________张卡片上;第三张卡片上的所有书组成的集合是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解毕业班学业水平考试学生的数学考试情况,抽取了该校100名学生的数学成绩,将所有数据整理后,画出了样频率分布直方图(所图所示),若第1组第9组的频率各为x.

(1)求x的值,并估计这次学业水平考试数学成绩的众数;
(2)若全校有1500名学生参加了此次考试,估计成绩在[80,100)分内的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com