
分析 利用变换公式化简,代入求解即可.
解答 解:由$φ:\left\{{\begin{array}{l}{{x^'}=\frac{1}{3}x}\\{{y^'}=\frac{1}{2}y}\end{array}}\right.$得:$\left\{{\begin{array}{l}{x=3{x^'}}\\{y=2{y^'}}\end{array}}\right.$,代入$\frac{x^2}{9}+\frac{y^2}{4}=1$中得:$\frac{{{{(3{x^'})}^2}}}{9}+\frac{{{{(2{y^'})}^2}}}{4}=1$,
∴经过伸缩变换后的曲线方程为:x′2+y′2=1.
它表示圆心在原点,半径为1的圆.
点评 本题考查变换的运算法则,考查计算能力.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (5,2) | B. | (-5,-2) | C. | (-1,2) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-6-4$\sqrt{2}$,0)∪(0,+∞) | B. | (-6+4$\sqrt{2}$,0)∪(0,+∞) | C. | (-6+4$\sqrt{2}$,0) | D. | (-6-4$\sqrt{2}$,-6+4$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 概率是频率的稳定值,频率是概率的近似值 | |
| B. | 已知事件M⊆N,则当M发生时,N一定发生 | |
| C. | 若A,B为互斥事件,则P(A)+P(B)<1 | |
| D. | 若一生产厂家称,我们厂生产的产品合格率是0.98,则任取一件该产品,其是合格品的可能性大小为98% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
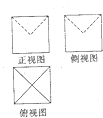 某几何体的三视图如图所示,图中的四边形是边长为2的正方形,其中正视图、侧视图中的两条虚线互相垂直,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形是边长为2的正方形,其中正视图、侧视图中的两条虚线互相垂直,则该几何体的体积是( )| A. | $\frac{20}{3}$ | B. | 6 | C. | $\frac{16}{3}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (0,1) | C. | (1,5) | D. | [1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [3,4] | B. | [5,7] | C. | [4,6] | D. | [7,8] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com