
| A. | [3,4] | B. | [5,7] | C. | [4,6] | D. | [7,8] |
分析 求出原函数的导函数,求得导函数的零点1,a-1,然后分1与a-1的大小分析导函数在不同区间内的符号,从而得到原函数在不同区间内的单调性,最后借助于已知条件得到a-1与3和5的关系,则答案可求.
解答 解:由f(x)=$\frac{1}{3}$x3-$\frac{1}{2}$ax2+(a-1)x+1得f′(x)=x2-ax+a-1,
令f′(x)=0,解得x=1或x=a-1.
当a-1≤1,即a≤2时,f′(x)在(1,+∞)上大于0,函数f(x)在(1,+∞)上为增函数,不合题意;
当a-1>1,即a>2时,f′(x)在(-∞,1)上大于0,函数f(x)在(-∞,1)上为增函数,
f′(x)在(1,a-1)内小于0,函数f(x)在(1,a-1)内为减函数,f′(x)在(a-1,+∞)内大于0,
函数f(x)在(a-1,+∞)上为增函数.
依题意应有:
当x∈(2,3)时,f′(x)<0,
当x∈(5,+∞)时,f′(x)>0.
∴3≤a-1≤5,解得4≤a≤6.
∴a的取值范围是[4,6].
故选:C.
点评 本题考查了利用导数研究函数的单调性,考查了分类讨论的数学思想方法,采用了逆向思维方法,解答的关键是对端点值的取舍,是中档题.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2n(n∈Z) | B. | 2n-1(n∈Z) | C. | 4n+1(n∈Z) | D. | 4n-1(n∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,e4) | D. | (e4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
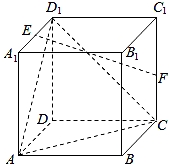 在正方体ABCD-A1B1C1D1中,E,F分别为A1D1和CC1的中点.
在正方体ABCD-A1B1C1D1中,E,F分别为A1D1和CC1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com