
分析 连结BD,根据余弦定理列出方程解出cosA(或cosC),进而给出sinA,sinC,代入面积公式即可.
解答 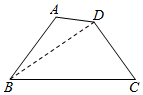 解:连结BD,
解:连结BD,
在△ABD中,BD2=AB2+AD2-2AB•ADcosA=5-4cosA,
在△BCD中,BD2=BC2+CD2-2BC•CDcosC=13-12cosC.
∴5-4cosA=13-12cosC,
∵A+C=180°,
∴cosA=-cosC.
∴cosA=-$\frac{1}{2}$.
∴sinA=sinC=$\frac{\sqrt{3}}{2}$.
∴四边形ABCD的面积S=S△ABD+S△BCD=$\frac{1}{2}$AB×AD×sinA+$\frac{1}{2}$BC×CD×sinC=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题考查了余弦定理在解三角形中的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [-1,-$\frac{1}{2}$] | B. | [-1,0] | C. | [0,1] | D. | [1,$\frac{3}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 气温x(℃) | 18 | 13 | 10 | -1 |
| 用电量y(度) | 24 | 34 | 38 | 64 |
| A. | 68 | B. | 67 | C. | 66 | D. | 65 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com