
| A. | 函数g(x)的一条对称轴是$x=\frac{π}{4}$ | B. | 函数g(x)的一个对称中心是$(\frac{π}{2},0)$ | ||
| C. | 函数g(x)的一条对称轴是$x=\frac{π}{2}$ | D. | 函数g(x)的一个对称中心是$(\frac{π}{8},0)$ |
分析 利用诱导公式、函数y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的图象的对称性,判断各个选项是否正确,从而得出结论.
解答 解:将函数$y=2sin(\frac{2}{3}x+\frac{3π}{4})$图象上所有点的横坐标缩短为原来的$\frac{1}{3}$,
可得y=2sin(2x+$\frac{3π}{4}$)的图象,
然后纵坐标不变,再向右平移$\frac{π}{8}$个单位长度,
得到函数y=g(x)=2sin(2x-$\frac{π}{4}$+$\frac{3π}{4}$)=2cos2x的图象,
令x=$\frac{π}{4}$,求得g(x)=0,
可得($\frac{π}{4}$,0)是g(x)的一个对称中心,故排除A;
令x=$\frac{π}{2}$,求得g(x)=-1,
可得x=$\frac{π}{2}$是g(x)的图象的一条对称轴,故排除B,故C正确;
令x=$\frac{π}{8}$,求得g(x)=$\sqrt{2}$,可得x=$\frac{π}{8}$不是g(x)的图象的对称中心,故排除D,
故选:C.
点评 本题主要考查诱导公式、函数y=Asin(ωx+φ)的图象变换规律,以及正弦函数、余弦函数的图象的对称性,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | x+$\sqrt{3}$y-2=0 | B. | x+$\sqrt{3}$y-4=0 | C. | $\sqrt{3}$x+y-2=0 | D. | x+$\sqrt{3}$y-6=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
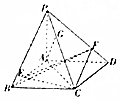 已知四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥平面ABCD,PA=AB=AC=2,AD=2$\sqrt{2}$,点E是线段AB上靠近B点的三等分点,点F、G分别在线段PD、PC上.
已知四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥平面ABCD,PA=AB=AC=2,AD=2$\sqrt{2}$,点E是线段AB上靠近B点的三等分点,点F、G分别在线段PD、PC上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
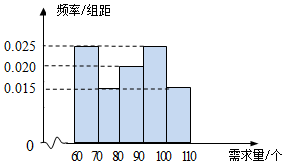 在某单位的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以x(单位:个,60≤x≤110)表示面包的需求量,T(单位:元)表示利润.
在某单位的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以x(单位:个,60≤x≤110)表示面包的需求量,T(单位:元)表示利润.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
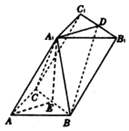 如图,在三棱柱ABC-A1B1C1中,D,E分别是B1C1、BC的中点,∠BAC=90°,AB=AC=2,A1A=4,A1E=$\sqrt{14}$.
如图,在三棱柱ABC-A1B1C1中,D,E分别是B1C1、BC的中点,∠BAC=90°,AB=AC=2,A1A=4,A1E=$\sqrt{14}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com