
(本小题满分14分)已知一个数列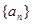 的各项都是1或2.首项为1,且在第
的各项都是1或2.首项为1,且在第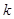 个1和第
个1和第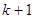 个1之间有
个1之间有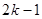 个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前
个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前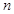 项的和为
项的和为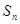 .参考:31×32=992,32×33=1056,44×45=1980,45×46=2070
.参考:31×32=992,32×33=1056,44×45=1980,45×46=2070
(I)试问第10个1为该数列的第几项?
(II)求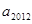 和
和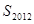 ;
;
(III)是否存在正整数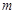 ,使得
,使得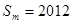 ?如果存在,求出
?如果存在,求出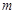 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
(I)91(项);(II) ;
;
(III)存在 =993+29=1022,使
=993+29=1022,使 .
.
解析试题分析:(1)根据题意将第 个1与第
个1与第 个1前的2记为第
个1前的2记为第 对,那么结合已知条件得到前
对,那么结合已知条件得到前 对共有项数为
对共有项数为
(2)因44×45=1980,45×46=2070,2012-1980=32,
故第2012项在第45对中的第32个数。
(3)由于前k对所在全部项的和为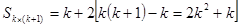 ,可知结论。
,可知结论。
解:将第 个1与第
个1与第 个1前的2记为第
个1前的2记为第 对,
对,
即 为第1对,共
为第1对,共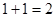 项;
项; 为第2对,共
为第2对,共 项;……;
项;……;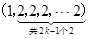 为第
为第 对,共
对,共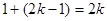 项;
项;
故前 对共有项数为
对共有项数为 .
.
(I)第10个1所在的项之前共有9对,所以10个1为该数列的
9×(9+1)+1=91(项) …………3分
(II)因44×45=1980,45×46=2070,2012-1980=32,
故第2012项在第45对中的第32个数,从而
又前2012项中共有45个1,其余2012-45=1967个数均为2,
于是 ……………………7分
……………………7分
(III)前k对所在全部项的和为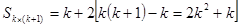 ,易得,
,易得, ,
, ,
,
即 且自第994项到第1056项均为2,而2012-1954=58能被2整除,
且自第994项到第1056项均为2,而2012-1954=58能被2整除,
故存在 =993+29=1022,使
=993+29=1022,使 . ……………………14分
. ……………………14分
考点:本试题主要考查了观察法求数列的通项公式,数列求和方法等知识,解题时要善于发现规律,层层深入的解决问题,要有较强的运算能力。
点评:解决该试题的关键是先将数列分组,便于发现规律,如分为(1,2),(1,2,2,2),(1,2,2,2,2,2)…,每组的项数构成数列2,4,6,…,发现将第 个1与第
个1与第 个1前的2记为第
个1前的2记为第 对,则前
对,则前 对共有项数为
对共有项数为 最后数列分组求和即可。
最后数列分组求和即可。


科目:高中数学 来源: 题型:填空题
在一次珠宝展览会上,某商家展出一套珠宝首饰,第一件首饰是1颗珠宝, 第二件首饰是由6颗珠宝(图中圆圈表示珠宝)构成如图1所示的正六边形, 第三件首饰如图2, 第四件首饰如图3, 第五件首饰如图4, 以后每件首饰都在前一件上,按照这种规律增加一定数量的珠宝,使它构成更大的正六变形,依此推断第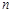 件首饰所用珠宝数为 颗.
件首饰所用珠宝数为 颗. 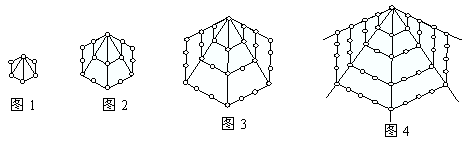
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
数列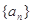 的前n项和记为
的前n项和记为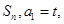 点
点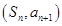 在直线
在直线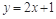 上,
上,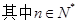 .(1)若数列
.(1)若数列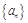 是等比数列,求实数
是等比数列,求实数 的值;
的值;
(2)设各项均不为0的数列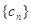 中,所有满足
中,所有满足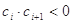 的整数
的整数 的个数称为这个数列
的个数称为这个数列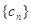 的“积异号数”,令
的“积异号数”,令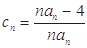 (
(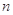
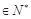 ),在(1)的条件下,求数列
),在(1)的条件下,求数列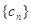 的“积异号数”
的“积异号数”
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知集合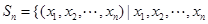 是正整数
是正整数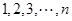 的一个排列
的一个排列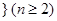 ,函数
,函数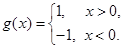 对于
对于 ,定义:
,定义: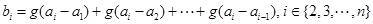 ,
,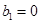 ,称
,称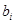 为
为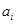 的满意指数.排列
的满意指数.排列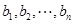 为排列
为排列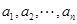 的生成列;排列
的生成列;排列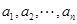 为排列
为排列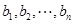 的母列.
的母列.
(Ⅰ)当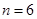 时,写出排列
时,写出排列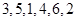 的生成列及排列
的生成列及排列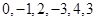 的母列;
的母列;
(Ⅱ)证明:若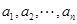 和
和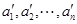 为
为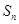 中两个不同排列,则它们的生成列也不同;
中两个不同排列,则它们的生成列也不同;
(Ⅲ)对于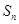 中的排列
中的排列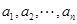 ,定义变换
,定义变换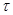 :将排列
:将排列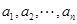 从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:一定可以经过有限次变换
从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:一定可以经过有限次变换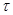 将排列
将排列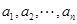 变换为各项满意指数均为非负数的排列.
变换为各项满意指数均为非负数的排列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com