
| A. | 有最大值$\frac{1}{2}$ | B. | 有最小值$\frac{1}{2}$ | C. | 有最大值$\frac{1}{4}$ | D. | 有最小值$\frac{1}{4}$ |
分析 根据题意在平面直角坐标系中,画出单位圆O,并设单位圆交x轴Q,交y轴P,然后分别过P,Q作x轴,y轴的平行线交于D点,可知点M在线段DQ上,点N在线段DP上,从而可表示出△OMN的面积为$\frac{1}{2}-\frac{1}{4}sin2θ$,从而可判断出△OMN有最小值,并可得出该最小值.
解答 解:如图单位圆O与x轴交于P,与y轴交于Q,过M,N作y轴和x轴的平行线交于D,则: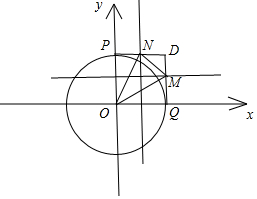
S△OMN=S正方形OPDQ-S△OPN-S△OMQ-S△DMN
=$1-\frac{1}{2}cosθ-\frac{1}{2}sinθ-\frac{1}{2}(1-cosθ)(1-sinθ)$
=$1-\frac{1}{2}-\frac{1}{2}sinθcosθ$
=$\frac{1}{2}-\frac{1}{4}sin2θ$;
∵$θ∈(0,\frac{π}{2})$;
∴2θ∈(0,π);
∴$2θ=\frac{π}{2}$时,△OMN的面积取最小值$\frac{1}{4}$.
故选:D.
点评 考查利用单位圆解决问题的方法,数形结合解题的方法,二倍角的正弦公式,以及三角形的面积公式,正弦函数的最值.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+x3 | B. | -x2+x3 | C. | x2-x3 | D. | -x2-x3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(0)>f(1) | B. | f(-1)<f(-3) | C. | f(-1)<f(1) | D. | f(-3)>f(-5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com