
| C | 2 6 |
| 6 |
| 21+14+7 |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 7 |
| 3 |
| 15 |
| 1 |
| 5 |


科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
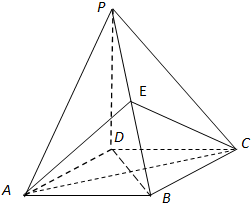 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 1+a1 |
| 1 |
| 1+a2 |
| 1 |
| 1+a3 |
| 1 |
| 1+an |
查看答案和解析>>
科目:高中数学 来源: 题型:
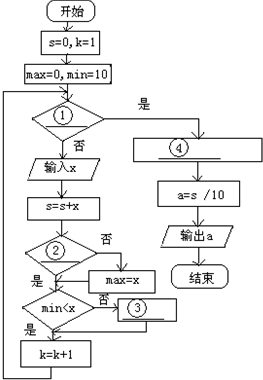 “钦州一中好声音”共有4名教师选手进入决赛,请了12名评委,在计算每位选手的平均分数时,去掉一个最高分和一个最低分后再求平均分.以下是一个程序框图,设计了一个算法,用循环语句完成这12个分数的输入,累加变量求和后减去最大数与最小数再求平均值.(假定分数采用10分制,即每位选手的分数最高分为10分,最低分为0分).
“钦州一中好声音”共有4名教师选手进入决赛,请了12名评委,在计算每位选手的平均分数时,去掉一个最高分和一个最低分后再求平均分.以下是一个程序框图,设计了一个算法,用循环语句完成这12个分数的输入,累加变量求和后减去最大数与最小数再求平均值.(假定分数采用10分制,即每位选手的分数最高分为10分,最低分为0分).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com